Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp :
+) Kẻ AD ⊥ B’C, xác định góc giữa mặt phẳng (AB’C) và mặt phẳng (BCC’B’)
+) Tính BB’.
+) Tính thể tích khối lăng trụ và suy ra thế tích AB’CA’C’
Cách giải :
Gọi H là trung điểm của BC ta có
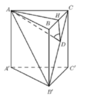
Trong (AB’C) kẻ AD ⊥ B’C
Ta có:
=> ((AB'C);(BCC'B')) = (AD;HD) = ADH
Ta có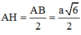 
Dễ thấy ∆CBB’ đồng dạng với ∆CDH (g.g)
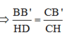
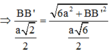
Ta có: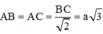 
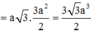
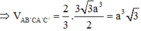
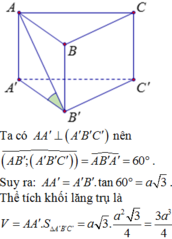
Đáp án A
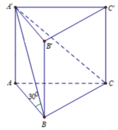
Ta có: A ' A = A B tan 30 ∘ = 3 a . 1 3 = a 3 ; S A B C = 1 2 3 a 2 = 9 a 2 2
Thể tích khối chóp A’.ABC là V = 1 3 A ' A . S A B C = 1 3 a 3 . 9 a 2 2 = 3 3 a 3 2 .
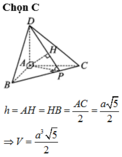
Đáp án A
Ta có
A B = B C = A C 2 = a ⇒ S A B C = a 2 2 ⇒ V = S h = a 3 2
Đáp án A.
Ta có B A ⊥ AA ' B A ⊥ AC ⇒ B A ⊥ A C C ' A '
Do đó góc giữa BC’ và (AA’C) bằng A C ' A ^ = 30 0
Khi đó A C ' tan 30 0 = A B ⇒ A C ' = A B tan 30 0
Mặt khác A B = A C tan C = a 3 ⇒ A C ' = 3 a .
⇒ C C ' = A C ' 2 − A C 2 = 2 a 2 ⇒ V = S A B C . C C ' = A B . A C 2 . C C ' = a 3 6.