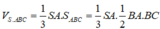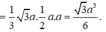Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
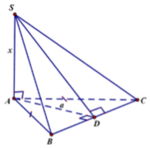
Đặt SA = x > 0. Ta có ![]() Ta có:
Ta có:
![]()
![]()
Xét tam giác vuông SBD, ta có ![]()
Khi đó: ![]()
Vậy ![]()

Chọn D
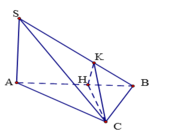
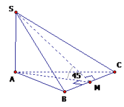
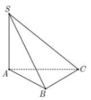
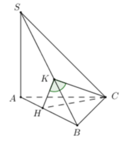
Từ C kẻ CH ⊥ AB tại H. Từ H kẻ HK ⊥ SB tại K.
+ Giao tuyến của hai mặt phẳng (SBC) và (SAB) là SB.
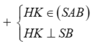
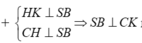
mà CK ∈ (SBC)
Do đó góc giữa hai mặt phẳng (SBC) và (SAB) là C K H ^ = 30 O
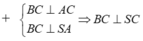
Tam giác SBC vuông tại C có góc B S C ^ = 60 O nên
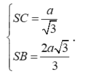
+ Tam giác SBC vuông tại C có CK là đường cao nên
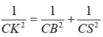
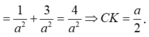
+ Tam giác CKH vuông tại H (vì CH ⊥ (SAB)) và C K H ^ = 30 O có nên
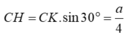
+ Tam giác ABC vuông tại C và có CH là đường cao nên
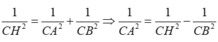
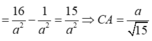
+ Tam giác ABC vuông tại C nên
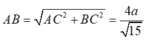
+ Tam giác SAB vuông tại nên A
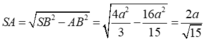
Thể tích khối chóp là
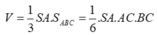
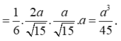

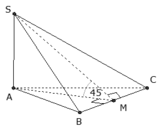
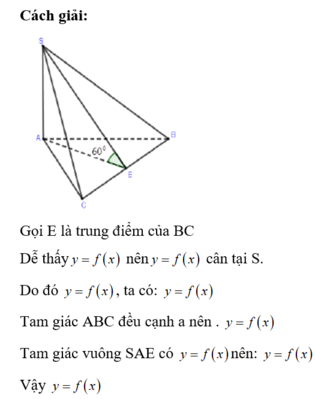
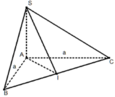
1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
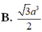
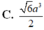
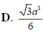

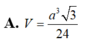
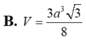
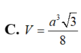
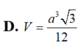

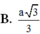
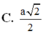
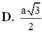

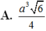
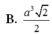
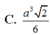
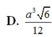

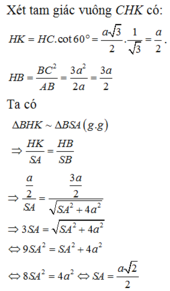
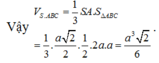


Chọn D
Có
Vậy