Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tứ giác ABEC : AB // DC hay AB // DE
AB = CE (=DC)
=> tứ giác ABEC là hình bình hành (1)
b) tam giác BCE vuông cân tại C và CK _|_ BE => KB=KE
tam giác DBE: CD = CE và KB = KE => KC // BD
và KC = IB ( = 1/2 * BD)
=> KC //= IB => tứ giác BICK là hbh . Mà CKB^ = 90o => BICK là hcn Mặt khác IC = IB => BICK là hình vuông (2)
(1) => O là trung điểm của BC . Mà (2) => O cũng là trung điểm của IK
Hay I,O,K thẳng hàng
d) chịu!

a)Có hình vuông ABCD=> AB=CD mà CD=CE(gt)=>AB=CE(1)
Có hình vuông ABCD=>AB//CD mà do D đôi xứng với E qua C=>D,E,C thẳng hàng=> AB//CE(2)
Từ (1) và(2)=> tứ giác ABEC là hình bình hành (1 cặp cạnh đối song song bằng nhau)
b) Tứ giác BICK có
+góc BIC=900 (tính chất 2 đường chéo của hình vuông)
+góc BKC=90o(gt)
+góc ICK=900 (2 đường phân giác của 2 góc BCD và BCE kề bù)
=> Tứ giác BICK là hình chữ nhật
mà IB=IC(tính chất đường chéo của hình vuông)
=>HCN BICK là hình vuông
-Có BC và AE là đg chéo của HBH ABEC
-Có BC và IK làđg chéo của hình vuông BICK
=> BC giao IK giao AE= O
=> I;O;K thẳng hàng

a) Xét tứ giác ABCE có AB song song và bằng EC (gt) nên nó là hình bình hành.
b) Xét tứ giác ABED có AB song song và bằng DE (gt) nên nó là hình bình hành.
Lại có \(\widehat{ADE}=90^o\) nên ABED là hình chữ nhật.
Lại có AB = AD nên ABED là hình vuông.
c) Xét tam giác AME và DMB có :
ME = B
AE = DB (Hai đường chéo hình vuông)
\(\widehat{AEM}=\widehat{DBM}=45^o\) (ABED là hình vuông)
\(\Rightarrow\Delta AEM=\Delta DBM\left(c-g-c\right)\Rightarrow\widehat{MAE}=\widehat{MDB}\) (1)
Xét hai tam giác vuông AHI và DOI có:
\(\widehat{AIH}=\widehat{DIO}\) (Hai góc đối đỉnh)
\(\Rightarrow\widehat{HAI}=\widehat{IDO}\) (Cùng phụ với hai góc bên trên) (2)
Từ (1) và (2) ta có: \(\widehat{ODK}=\widehat{IDO}\) hay DO là tia phân giác của góc \(\widehat{IDK}\)
d) Xét tam giác IDK có DO là tia phân giác đồng thời là đường cao nên nó là tam giác cân tại D.Vậy thì DO là đường trung tuyến hay OI = OK.
Do ABED là hình vuông nên O là trung điểm BD.
Xét tứ giác DIBK có O là trung điểm hai đường chéo nên DIBK là hình bình hành.
Lại có \(IK\perp DB\) nên DIBK là hình thoi.

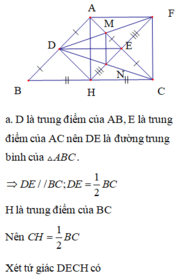
a: Xét tứ giác ADEF có
\(\widehat{ADE}=\widehat{AFE}=\widehat{DAF}=90^0\)
=>ADEF là hình chữ nhật
b: Xét ΔABC có
E là trung điểm của CB
ED//AB
Do đó: D là trung điểm của AC
Xét tứ giác AECK có
D là trung điểm chung của AC và EK
=>AECK là hình bình hành
Hình bình hành AECK có AC\(\perp\)EK
nên AECK là hình thoi
c: Xét ΔABC có
E,D lần lượt là trung điểm của CB,CA
=>ED là đường trung bình của ΔABC
=>\(ED=\dfrac{AB}{2}\)
mà \(ED=\dfrac{EK}{2}\)
nên EK=AB
Ta có: ED//AB
D\(\in\)EK
Do đó: EK//AB
Ta có: ADEF là hình chữ nhật
=>AE cắt DF tại trung điểm của mỗi đường
=>O là trung điểm chung của AE và DF
Xét tứ giác ABEK có
KE//AB
KE=AB
Do đó: ABEK là hình bình hành
=>AE cắt BK tại trung điểm của mỗi đường và AE=BK
mà O là trung điểm của AE
nên O là trung điểm của BK
=>B,O,K thẳng hàng
ΔEMA vuông tại M
mà MO là đường trung tuyến
nên \(MO=\dfrac{AE}{2}\)
mà AE=DF
nên \(MO=\dfrac{DF}{2}\)
Xét ΔDMF có
MO là đường trung tuyến
MO=DF/2
Do đó: ΔDMF vuông tại M
=>\(\widehat{DMF}=90^0\)