Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm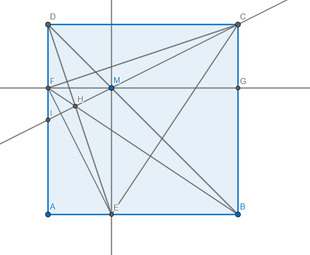

Gọi M là trung điểm BC => BM=CM
Xét tam giác ABC có:
BM=CM
AE=EC (giả thiết vì E la trung điểm của AC)
Nên: EM là đường trung bình trong tam giác ABC
=>EM//AB và EM=AB/2
Tương tự: Xét tam giác BCD có:
FM là đường trung bình trong tam giác BCD
=>FM//CD và FM=CD/2
Lại có:
FM//CD
mà AB//CD (theo giả thiết ABCD la hthang)
Nên: FM//AB
Mà EM//AB
Do đó, theo tiên đề Ơclit ta có: E,M,F thẳng hàng.
Vậy,EF=FM-EM=(CD-AB)/2


a) \(\Delta OCK\)vuông, \(CM\perp OK\) nên
\(KC^2=KM.KO\)
Kc là tiếp tuyến, KEF là cát tuyến nên
\(KC^2=KE.KF\)
Suy ra , \(KM.KO=KE.KF\)nên
\(\frac{KM}{KE}=\frac{KF}{KO}\)
Ta có \(\Delta KEM~\Delta KOF\)( c . g . c) nên\(\widehat{M_1}=\widehat{F_1}\) , từ đó EMOF là tứ giác nội tiếp.