Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

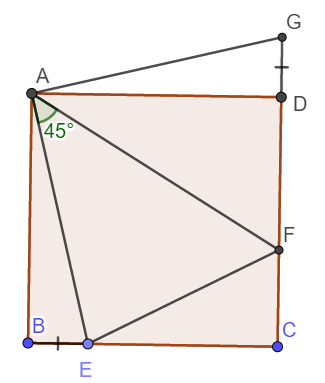
a) Xét tam giác vuông ABE và ADG có:
BE = DG (gt)
AB = AD
\(\Rightarrow\Delta ABE=\Delta ADG\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{BAE}=\widehat{DAG}\) (Hai góc tương ứng)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{DAG}+\widehat{FAD}\)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{FAG}\)
Mà \(\widehat{BAE}+\widehat{FAD}=90^o-\widehat{EAF}=45^o\) nên \(\widehat{FAG}=45^o\)
b) Do \(\Delta ABE=\Delta ADG\Rightarrow AE=AG\)
Xét tam giác AEF và AGF có:
AE = AG (cmt)
Cạnh AF chung
\(\widehat{EAF}=\widehat{GAF}\left(=45^o\right)\)
\(\Rightarrow\Delta AEF=\Delta AGF\left(c-g-c\right)\)
\(\Rightarrow EF=GF=FD+DG=FD+BE\)

Mình làm câu c thôi ( câu a,b mấy trang khác có nha). Hình mn tự vẽ nha.
Theo b, có: Tam giác DCE là tam giác đều
=> DCE=CDE=DEC=60
Xét tam giác CND:
Áp dụng định lí:" Tổng ba góc một tam giác bằng 180"
=>CND+CDN+DCN=180
=>CND+60+10=180 (vì ICD=10; CDE= 60)
=>CND=180-70=110 (1)
Xét tam giác CNE:
Áp dụng định lí:"Tổng ba góc một tam giác bằng 180"
=>CNE+CEN+NCE=180
=>CNE+60+(ACB+ECF)=180
=>CNE+60+30+20=180
=>CNE+110=180
=>CNE=70 (2)
Từ (1) và (2) suy ra: CND+CNE=70+110=180
=>DNE=180 =>DNE là góc bẹt
=>D; N; E thẳng hàng (ĐPCM)

a) xét tam giác ABM = DCM( c-g-c ) (*)
=) * góc BAD = góc ADC
=) AB // CD
* AB = DC ( 1 )
xét tam giác ABH= EBH ( c-g-c )
=) AB = BE ( 2 )
từ (1) và (2)=) CD=BE
b) ( đề sai, phải là CD vuông góc AC mới đúng )
từ (*) =) góc ABM = DCM
mà tg ABC vuông tại A=) ABM+ACB=90 độ
suy ra góc DCM+ACB=90 độ
=) CD vuông góc vs AC
c ) áp dụng trung tuyến cạnh huyền =) AM=1/2BC
d) Do AM = 1/2BC
=) BC = 10cm
áp dụng định lý py-ta-go cho tg ABC vuông tại A ta có:
AB^2 + AC^2 = BC^2
AB^2 = 36
AB = 6cm

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: ΔABD=ΔEBD
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
Xét ΔDAF và ΔDEC có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DF=DC
Do đó: ΔDAF=ΔDEC
=>AF=CE
c: Ta có: ΔDAF=ΔDEC
=>\(\widehat{DAF}=\widehat{DEC}\)
mà \(\widehat{DEC}=90^0\)
nên \(\widehat{DAF}=90^0\)
Ta có: \(\widehat{BAD}+\widehat{DAF}=\widehat{BAF}\)
=>\(\widehat{BAF}=90^0+90^0=180^0\)
=>B,A,F thẳng hàng
Xét ΔBFC có BA/AF=BE/EC
nên AE//FC