Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác vuông ABC, theo Pitago ta có: \(NC^2=NB^2+BC^2=x^2+a^2\)
Xét tam giác vuông NCF, chiều cao CB: Áp dụng hệ thức lượng ta có : \(NF=\frac{NC^2}{NB}=\frac{x^2+a^2}{x}\)
AN = a - x ; \(\frac{EA}{BC}=\frac{AN}{NB}\Rightarrow EA=\frac{a-x}{x}.a=\frac{a^2-ax}{x}\)
\(AF=AN+NF=a-x+\frac{a^2+x^2}{x}=\frac{ax+a^2}{x}\)
Vậy nên \(S_{ACEF}=S_{EAF}+S_{CAF}=\frac{1}{2}.AF.EA+\frac{1}{2}AF.BC\)
\(=\frac{1}{2}.\frac{ax+a^2}{x}.\left(\frac{a^2-ax}{x}+a\right)=\frac{1}{2}.\frac{ax+a^2}{x}.\frac{a^2}{x}=\frac{a^4+a^3x}{2x^2}\left(đvdt\right)\)
b) Ta có \(\frac{a^4+a^3x}{2x^2}=3a^2\Rightarrow a^2+ax-6x^2=0\)
\(\Rightarrow\left(a-2x\right)\left(a+3x\right)=0\)
Do a, x > 0 nên a = 2x hay N là trung điểm AB.

Câu hỏi của Vũ Huy Hiệu - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

b: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔBAD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra NP//MQ và NP=MQ
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC
mà AC\(\perp\)BD
nên QP\(\perp\)BD
mà MQ//BD
nên MQ\(\perp\)QP
hay \(\widehat{MQP}=90^0\)
Xét tứ giác MQPN có
MQ//NP
MQ=NP
Do đó: MQPN là hình bình hành
mà \(\widehat{MQP}=90^0\)
nên MQPN là hình chữ nhật
Xét tứ giác MQPN có
\(\widehat{MQP}+\widehat{MNP}=180^0\)
Do đó: MQPN là tứ giác nội tiếp
hay M,Q,P,N cùng thuộc 1 đường tròn

Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
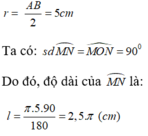

Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)
a) Có nhiều cách tính diện tích AICJ. Chẳng hạn:
C1: Do I, J là trung điểm AB, AD nên \(AI=AJ=\frac{1}{2}\)
Ta thấy ngay \(\Delta AJC=\Delta AIC\left(c-g-c\right)\Rightarrow S_{AJC}=S_{AIC}\)
Vậy thì \(S_{AICJ}=2S_{AIC}=2.\frac{1}{2}AI.CB=\frac{1}{2}\left(đvdt\right)\)
C2:
Do I, J là trung điểm AB, AD nên \(AI=AJ=\frac{1}{2}\)
Ta thấy ngay \(\Delta DJC=\Delta BIC\) (Hai cạnh góc vuông) \(\Rightarrow S_{DJC}=S_{BIC}\)
Vậy thì \(S_{AICJ}=S_{ABCD}-2S_{BIC}=1-\frac{1}{2}=\frac{1}{2}\left(đvdt\right)\)
b)
C1: Xét tam giác DJC có \(tan\widehat{DCJ}=\frac{JD}{DC}=\frac{1}{2}\Rightarrow\widehat{DCJ}\approx26^o34'\)
\(\Rightarrow\widehat{JCA}=45^o-\widehat{DCJ}\Rightarrow\widehat{ICJ}=90^o-2\widehat{DCJ}\)
Dúng máy tính ta tìm được \(\sin\widehat{ICJ}=\frac{3}{5}\)
C2: Theo Pytago thì \(JC=\sqrt{1+\frac{1}{4}}=\frac{\sqrt{5}}{2}\)
Ta thấy ngay \(S_{AIJ}=\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}\)
\(\Rightarrow S_{IJC}=\frac{1}{2}-\frac{1}{8}=\frac{3}{8}\)
Kẻ IH vuông góc JC.
Ta tìm được \(IH=2S_{IJC}:JC=2.\frac{3}{8}:\frac{\sqrt{5}}{2}=\frac{3\sqrt{5}}{10}\)
\(\Rightarrow\sin\widehat{ICJ}=\frac{IH}{IC}=\frac{3}{5}.\)