NL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
NL
1
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
Kẻ $Dt\parallel Ex\parallel Gy$ ($Dt$ nằm cùng phía với $Ex$ trên mặt phẳng bờ $DE$)
Vì $Dt\parallel Ex$ nên:
$\widehat{xED}+\widehat{EDt}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{EDt}=180^0-\widehat{xED}=180^0-120^0=60^0$
Vì $Dt\parallel Gy$ nên $\widehat{tDG}=\widehat{DGy}=30^0$ (2 góc so le trong)
$\Rightarrow \widehat{EDG}=\widehat{EDt}+\widehat{tDG}=60^0+30^0=90^0$
H
0
16 tháng 8 2023
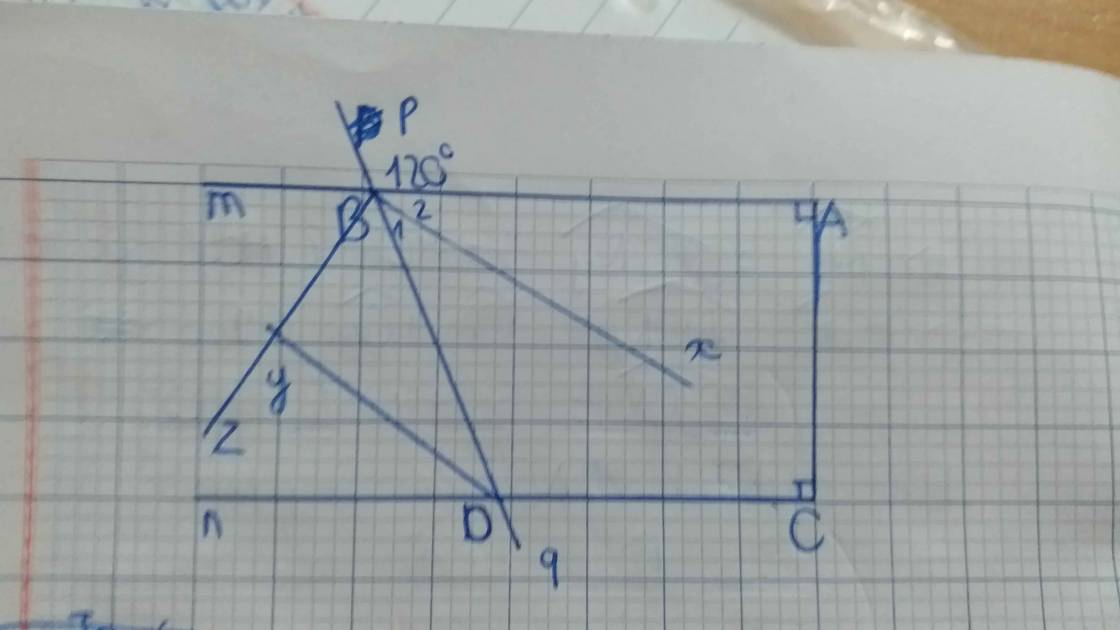
a: AB vuông góc AC
DC vuông góc AC
=>AB//DC
b: AB//CD
=>góc PBA=góc BDC
=>góc BDC=120 độ
góc BDn=180-120=60 độ
góc mBD=góc PBA=120 độ
góc mBP=góc ABD=180-120=60 độ
c: góc xBD=1/2*góc ABD=1/2*120=60 độ
góc yDB=1/2*góc BDn=1/2*120=60 độ
=>góc xBD=góc yDB
=>Bx//Dy
góc yBD+góc yDB
=1/2(góc mBD+góc nDB)
=1/2*180=90 độ
=>Bz vuông góc Dy
NH
1
F
4 tháng 10 2017
(ý bn cá hình nó vẽ như trên đúng ko)
Kẻ y // a (1)
=> góc CAO = góc AOy ( so le trong)
=> góc AOy = 30
Ta có góc AOB = góc AOy + góc yOB
=> góc yOB = góc AOB - góc AOy = 75 - 30 = 45
=> góc yOB = góc OBD( = 45 )
Mà 2 góc nằm ở vị trí so le trong
=> y//b (2)
Từ (1) và (2) => a//b
24 tháng 10 2021
Làm bài như con kặc ấy, OBD mày lấy đâu ra? COA=AOY mà COA - AOY=45°( what?) Rồi C mày lấy ở đâu? Làm như lồn ấy.
22 tháng 1 2018
mot hinh thang co dien h 420cm vuong , chieu cao 17,5cm , day lon hon day be 8cm . tinh do dai hai day cau hinh thang do
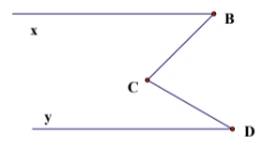
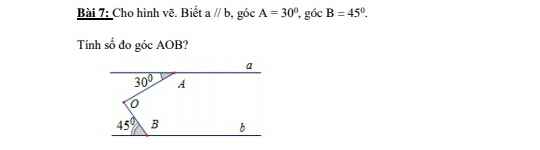
Vẽ tia Cz // Bx // Cy
Do Bx // Cz
⇒ ∠BCz = ∠xBC = 45⁰ (so le trong)
Do Cz // Dy
⇒ ∠DCz = ∠CDy = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCz + ∠DCz
= 45⁰ + 30⁰
= 75⁰