Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


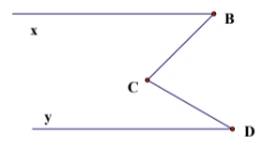
Vẽ tia Cz // Bx // Cy
Do Bx // Cz
⇒ ∠BCz = ∠xBC = 45⁰ (so le trong)
Do Cz // Dy
⇒ ∠DCz = ∠CDy = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCz + ∠DCz
= 45⁰ + 30⁰
= 75⁰

Lời giải:
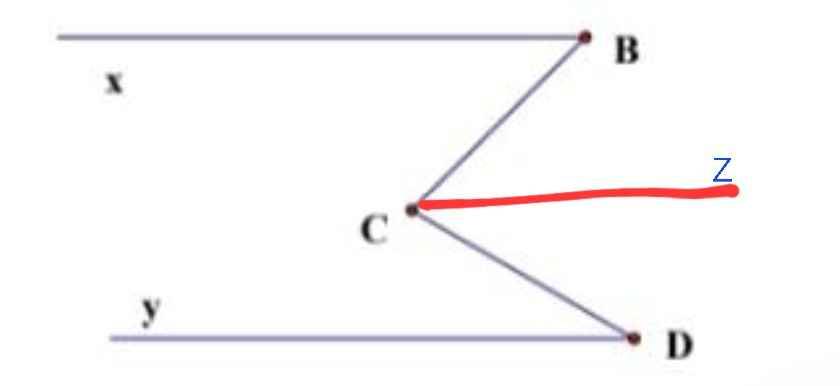
Kẻ $Dt\parallel Ex\parallel Gy$ ($Dt$ nằm cùng phía với $Ex$ trên mặt phẳng bờ $DE$)
Vì $Dt\parallel Ex$ nên:
$\widehat{xED}+\widehat{EDt}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{EDt}=180^0-\widehat{xED}=180^0-120^0=60^0$
Vì $Dt\parallel Gy$ nên $\widehat{tDG}=\widehat{DGy}=30^0$ (2 góc so le trong)
$\Rightarrow \widehat{EDG}=\widehat{EDt}+\widehat{tDG}=60^0+30^0=90^0$

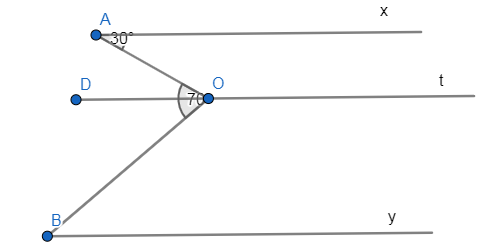
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)