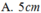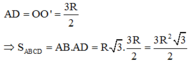Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

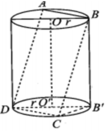
Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25
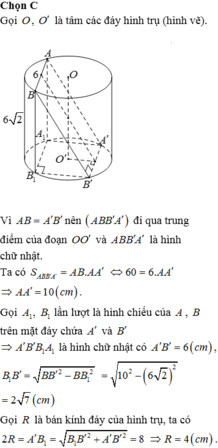
Gọi C C 1 và D D 1 là hai đường sinh của khối trụ
Khi đó D 1 C 1 / / = D C (1)
Đông thời ABCD là hình vuông nên AB//=DC (2)
Từ (1) và (2) suy ra AB//= D 1 C 1
Vậy A B C 1 D 1 nội tiếp đường tròn (O) nên A B C 1 D 1 là hình chữ nhật. Suy ra A C 1 là đường kính của (O)
Nghĩa là A C 1 = 2 r
Tam giác A B C 1 vuông ở B nên:
![]() (3)
(3)
Tam giác B C C 1 vuông ở C 1 nên:
![]() (4)
(4)
Từ (3) và (4) suy ra
![]()
Vậy diện tích hình vuông ABCD là S = A B 2 = 5 r 2 2
* Gọi α là góc hợp bởi mp(ABCD) và mặt phẳng đáy của hình trụ, ta có:
![]()
Với 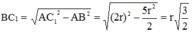
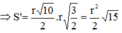
Mà A B C 1 D 1 là hình chiếu của ABCD trên mặt đáy hình trụ nên:
S
'
=
S
.
cos
α
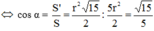

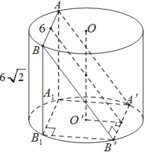
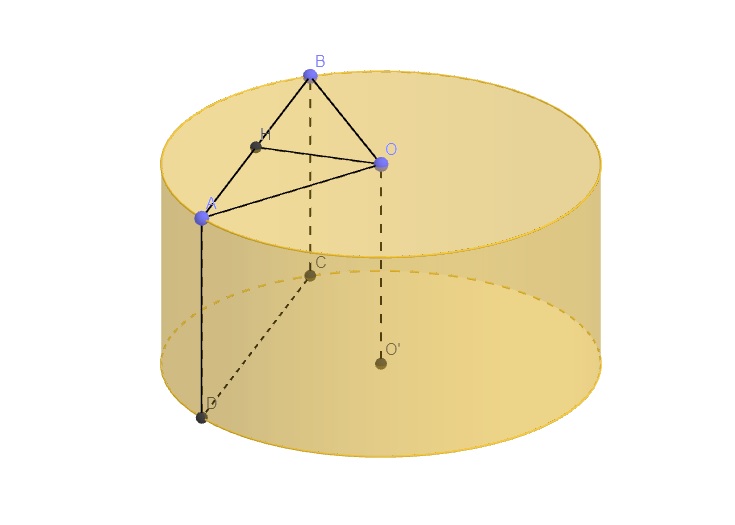
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\Rightarrow OH\perp\left(ABCD\right)\)
\(\Rightarrow V_{O.ABCD}=\dfrac{1}{3}OH.S_{ABCD}\)
Đặt \(OH=x\Rightarrow BH=\sqrt{R^2-OH^2}=\sqrt{9a^2-x^2}\)
\(\Rightarrow AB=2BH=2\sqrt{9a^2-x^2}\)
\(\Rightarrow V=\dfrac{1}{3}x.3a.2\sqrt{9a^2-x^2}=a.2x.\sqrt{9a^2-x^2}\le a\left(x^2+9a^2-x^2\right)=9a^3\)
\(\Rightarrow V_{max}=9a^3\)