Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương pháp: Lưu ý đề bài là “cắt đi”. Diện tích xung quanh của hình nón chính là diện tích hình quạt lớn hơn. Chu vi đáy chính là độ dài cung lớn A B ⏜ .
Cách giải: Diện tích xung quanh của hình nón là:

Vậy diện tích toàn phần của hình nón là:
![]()

Đáp án C
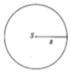
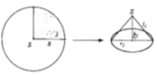
Gọi R = 10 và r lần lượt là bán kính đát của hình nón lớn và hình nón nhỏ.
Ta có:
r R = S M S O = S O − M O S O ⇔ r 10 = 3 5 ⇔ r = 6 c m
Diện tích xung quanh của hình nón nhỏ là S x q = π r S M 2 + r 2 = 36 π 26 c m 2

Đáp án D
Phương pháp:
- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.
- Tính diện tích S , S ' với chú ý S là diện tích hình tròn và S ' là diện tích xung quanh của hình nón.
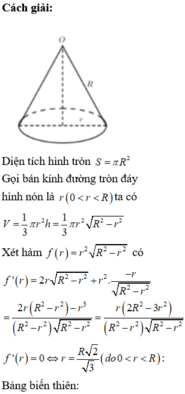
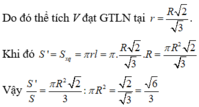

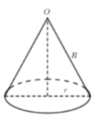
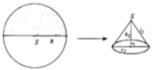
Diện tích hình tròn S = πR 2
Gọi bán kính đường tròn đáy hình nón là r(0<r<R) ta có
![]()
Xét hàm 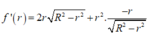
có 

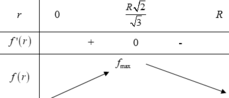
Bảng biến thiên:
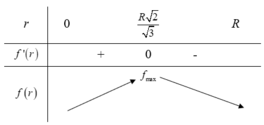
Do đó thể tích V đạt GTLN tại
r
=
R
2
3
. Khi đó
![]()
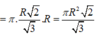
Vậy 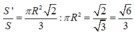
Chọn đáp án D.

Đáp án A.
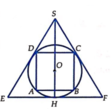
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .

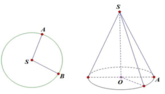

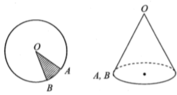



Hình nón được tạo thành có độ dài đường sinh là l = OA = 2, chu vi đường tròn đáy bằng độ dài cung AB và bằng