Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.
- Tính diện tích S , S ' với chú ý S là diện tích hình tròn và S ' là diện tích xung quanh của hình nón.
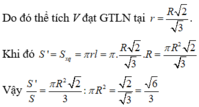

Chọn D.
Phương pháp:

Cách giải:
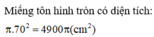
Gọi bán kính đáy và chiều cao của hình nón lần lượt là r , h ( r , h > 0 ) .

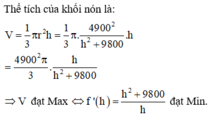
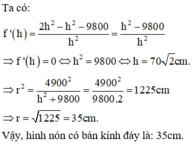

Đáp án D
Gọi r;h lần lượt là bán kính đáy và chiều cao của khối nón ⇒ V N = 1 3 π r 2 h
Mà h = l 2 − r 2 = R 2 − r 2 = 81 − r 2 Suy ra V N = 1 3 π r 2 81 − r 2 = π 3 r 4 81 − r 2
Ta có r 2 . r 2 . 162 − 2 r 2 2 ≤ r 2 + r 2 + 162 − 2 r 2 3 2.27 = 78732 ⇒ V ≤ π 3 . 78732 ⇒ V max = 78732 3 π
Dấu " = " xaye ra ⇔ 3 r 2 = 162 ⇔ r = 3 6 ⇒ Độ dài cung tròn là l = 2 π r = 6 π 6

Đáp án D.
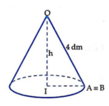
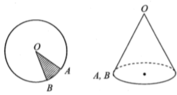
Cung AB có bán kính O A = 4 d m và số đo bằng π 2 r a d nên có độ dài là l A B = π 2 .4 = 2 π d m .
Từ giả thiết ta có đỉnh của hình nón là O, đường sinh O A = 4 d m và chu vi đáy hình nón là C = l A B = 2 π d m .
Gọi I là tâm đáy, khi đó bán kính đáy của hình nón là r = I A = C 2 π = 2 π 2 π = 1 (dm).
Do vuông tại I nên ta có O A 2 = O I 2 + I A 2 ⇒ h = O I = O A 2 − I A 2
⇒ h = 4 2 − 1 2 = 15 ≈ 3,873 (dm).

Đáp án B
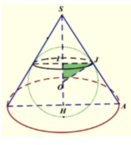
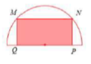
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

Đáp án B
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

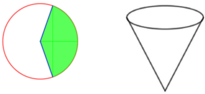
Thể tích cái phễu là V = 1 3 πr 2 h
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A

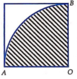
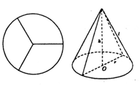

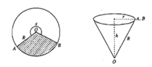
Diện tích hình tròn S = πR 2
Gọi bán kính đường tròn đáy hình nón là r(0<r<R) ta có
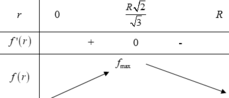
Xét hàm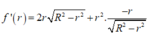
có
Bảng biến thiên:
Do đó thể tích V đạt GTLN tại r = R 2 3 . Khi đó
Vậy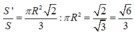
Chọn đáp án D.