Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
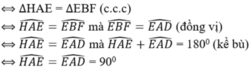
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.

Tự vẽ hình
a) Ta có: AB = CD (cạnh hình thoi)
BE = DG (g.t)
=> AB + BE = CD + DG hay AE = CG (cmt)
Xét tam giác AHE và tam giác CFG ta có:
AE=CG
HAE = FCG (cùng bù vs BAD = DCB)
AH=CF (gt)
Do đó tam giác AHE = tam giác CFG (c.g.c) => HE = FG
Do đó EFGH là cạnh bình hành (đpcm)
b) Nối E vs G
Xét tam giác OBE và tam giác ODG ta có:
BE= DG (gt)
OBE = ODG (so le trong)
OB = OD ( tính chất đường chéo của hình thoi ABCD)
=> tam giác OBE = tam giác ODG (c.g.c) => OBE = ODG
Mà DOG + GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
\(\Leftrightarrow\Delta HAE=\Delta EBF\left(c.c.c\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EBF}=\widehat{EDA}\left(đv\right)\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}\) mà \(\widehat{HAE}+\widehat{EAD=180^O\left(kb\right)}\)
\(\Leftrightarrow\widehat{HAE}=\widehat{EAD}=90^O\)
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
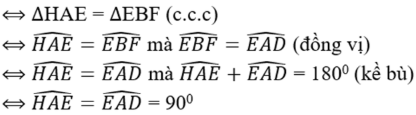
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.

1:
ta có:ABCD là hình thoi
=>\(\widehat{BAD}=\widehat{BCD};\widehat{ABC}=\widehat{ADC}\)
Ta có: \(\widehat{BAD}+\widehat{EAH}=180^0\)(hai góc kề bù)
\(\widehat{BCD}+\widehat{FCD}=180^0\)(hai góc kề bù)
mà \(\widehat{BAD}=\widehat{BCD}\)
nên \(\widehat{EAH}=\widehat{FCD}\)
Ta có: \(\widehat{ABC}+\widehat{EBC}=180^0\)(hai góc kề bù)
\(\widehat{ADC}+\widehat{ADG}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ADC}\)
nên \(\widehat{EBC}=\widehat{ADG}\)
Ta có: \(DA+AH=DH\)
\(AB+BE=AE\)
\(BC+CF=BF\)
\(CD+DG=CG\)
mà DA=AB=BC=CD và AH=BE=CF=DG
nên DH=AE=BF=CG
Xét ΔHAE và ΔFCG có
HA=FC
\(\widehat{HAE}=\widehat{FCG}\)
AE=CG
Do đó: ΔHAE=ΔFCG
=>HE=FG
Xét ΔHDG và ΔFBE có
DH=BF
\(\widehat{HDG}=\widehat{BFE}\)
DG=BE
Do đó: ΔHDG=ΔFBE
=>HG=FE
Xét tứ giác GHEF có
GH=EF
GF=HE
Do đó: GHEF là hình bình hành
2: Gọi O là giao điểm của AC và BD
Ta có: ABCD là hình thoi
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét tứ giác AHCF có
AH//CF
AH=CF
Do đó: AHCF là hình bình hành
=>AC cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểmcủa HF
Ta có: EHGF là hình bình hành
=>EG cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của HF
nên O là trung điểm của EG
=>Hình bình hành EHGF và hình thoi ABCD có chung tâm

1: DH=DA+AH
CG=CD+DG
BF=BC+CF
AE=AB+BE
mà DA=CD=BC=AB và AH=DG=CF=BE
nên DH=CG=BF=AE
góc ADG=180 độ-góc ADC
góc EBF=180 độ-góc ABC
mà góc ADC=góc ABC
nên góc ADG=góc EBF
góc EAB=180 độ-góc BAD
góc GCF=180 độ-góc BCD
mà góc BAD=góc BCD
nên góc EAB=góc GCF
Xét ΔHDG và ΔFBE có
HD=FB
góc HDG=góc FBE
DG=BE
Do đó: ΔHDG=ΔFBE
=>HG=FE
Xét ΔHAE và ΔFCG có
HA=FC
góc HAE=góc FCG
AE=CG
Do đó: ΔHAE=ΔFCG
=>HE=FG
Xét ΔADG và ΔCBE có
AD=CB
góc ADG=góc CBE
DG=BE
Do đó: ΔADG=ΔCBE
=>AG=CE
Xét tứ giác EHGF có
EH=FG
EF=GH
Do đó: EHGF là hình bình hành
2:
Gọi O là giao của AC và BD
ABCD là hình thoi
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét tứ giác AGCE có
AG=CE
AE=CG
Do đó: AGCE là hình bình hành
=>AC cắt GE tại trung điểm của mỗi đường
=>O là trung điểm của GE
GHEF là hình bình hành
=>GE cắt HF tại trung điểm của mỗi đường
=>O là trung điểm của HF
=>ĐPCM
3:
ABCD là hình vuông
=>góc BAD=góc ADC=90 độ
Xét ΔHAE vuông tại A và ΔGDH vuông tại D có
HA=GD
AE=DH
Do đó: ΔHAE=ΔGDH
=>HE=GH
Xét hình bình hành EHGF có HE=GH
nên EHGF là hình thoi
hơi sai