Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)


+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)

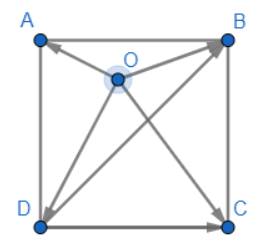
Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại

1: \(=\left|\overrightarrow{CO}-\overrightarrow{CB}\right|=BO=\dfrac{a\sqrt{2}}{2}\)

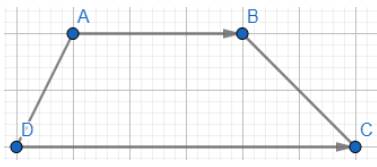
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.

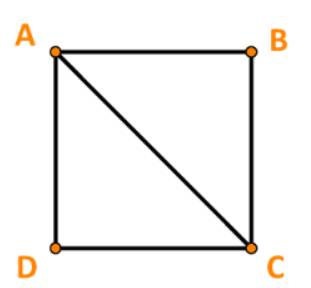
Ta có: \(|\overrightarrow {AB} | = AB\) và \(|\overrightarrow {AC} |\; = AC.\)
Mà \(AB = 3,\;AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)
\( \Rightarrow \;|\overrightarrow {AB} |\, = 3;\;\;|\overrightarrow {AC} |\, = 3\sqrt 2 \)

Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.

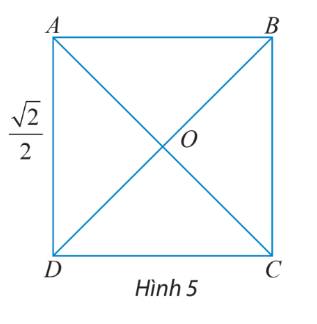
Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = 1\)
\(OA = \frac{1}{2}AC = \frac{1}{2}\)
Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\)


Tham khảo:
\(\overrightarrow {CD} = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).
\(\begin{array}{l} \Rightarrow \overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)
Xét tam giác ABC, ta có:
\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)
\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)
Vậy \(\left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = 1.\)
Dựa vào tính chất kết hợp, ta có:
\(\begin{array}{l}\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} = \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) + \overrightarrow {BA} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)