Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Hai tam giác vuông BHD và BKD có:
BD là cạnh chung
\(\widehat{HDB}=\widehat{KDB}\) (ABCD là hình thoi)
Vậy \(\Delta BHD=\Delta BKD\) (cạnh huyền - góc nhọn)
\(\Rightarrow\) BH = BK (hai cạnh tương ứng)
Chứng minh tương tự, ta cũng có: \(\Delta BPD=\Delta BQD\) (cạnh huyền - góc nhọn)
\(\Rightarrow\) DP = PQ (hai cạnh tương ứng)
b) Tứ giác HBQD có:
BQ // HD (AD // BC, H \(\in\) AD, Q \(\in\) BC)
BH // QD (BH \(\perp\) AD, QD \(\perp\) BC, AD // BC)
\(\Rightarrow\) HBQD là hình bình hành.
mà \(\widehat{BHD}=90^o\) (\(\Delta BHD\) vuông tại H)
\(\Rightarrow\) HBQD là hình chữ nhật.
c) Tứ giác BPDK có:
BP // DK (AB // CD, P \(\in\) AB, K \(\in\) CD)
BK // PD (BK \(\perp\) CD, PD\(\perp\) AB, AB // CD)
\(\Rightarrow\) BPDK là hình bình hành.
mà \(\widehat{BPD}=90^o\) (\(\Delta BPD\) vuông tại P)
\(\Rightarrow\) BPDK là hình chữ nhật.
\(\Rightarrow\) PK = BD và PK \(\cap\) BD tại trung điểm của BD. (1)
Lại có: HBQD là hình chữ nhật (cm câu b)
\(\Rightarrow\) HQ = BD và HQ \(\cap\) BD tại trung điểm của BD. (2)
Từ (1) và (2) \(\Rightarrow\) PK = HQ = BD và chúng đồng quy.

Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

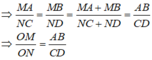

Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
S A E O = S B F O (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
S D E O = S C F O (2)
Từ (1) và (2) suy ra : S O A D = S O B C (3)
Suy ra: OH.AD = OK.BC
⇔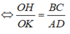

a: Xét ΔAHB vuông tại H và ΔDAB vuông tại A có
góc ABH chung
=>ΔAHB đồng dạng vơi ΔDAB
b: \(BD=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=7,2cm
AH=12*16/20=9,6cm
