YN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YN
0
YN
3
CC
29 tháng 2 2020
Gọi O là giao điểm của 2 đường chéo của hình thoi
\(\Rightarrow\)O là trung điểm của AC và BD
\(\Rightarrow OA=\frac{1}{2}AC=\frac{1}{2}.8=4\left(cm\right)\)và \(OB=\frac{1}{2}BD=\frac{1}{2}.6=3\left(cm\right)\)
Tứ giác ABCD là hình thoi \(\Rightarrow AC\perp BD\)\(\Rightarrow OA\perp OB\)\(\Rightarrow\Delta OAB\)vuông tại O
Áp dụng định lý Pytago ta có: \(OA^2+OB^2=AB^2\)
\(\Rightarrow AB^2=4^2+3^2=16+9=25\)\(\Rightarrow AB=5\left(cm\right)\)
Vì ABCD là hình thoi \(\Rightarrow AB=BC=CD=CA\)
\(\Rightarrow P_{ABCD}=4.AB=4.5=20\left(cm\right)\)
29 tháng 2 2020
\(S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot8\cdot16=64\left(cm^2\right)\)
CM
15 tháng 11 2017
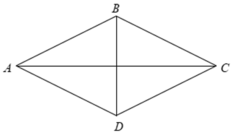
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :
L
25 tháng 2 2021
bạn tự vẽ hình nha ( mình nản vẽ hình lắm )
ta có AB = 6 cm
lại có góc ABC = 60 độ
suy ra : △ABC là △ đều ( △cân có một góc bằng 60 độ )
suy ra AC bằng 6 cm suy ra AO = CO = 3 cm
xét △ABO vuông tại O có :
theo định lý py-ta-go ta có AB2 = BO2+ AO2
=> BO2 = 36 - 9 = 25 (cm)
=> BO = 5 cm
=> BD = 10 cm
vậy diện tích hình thoi là:
1/2.6.10 = 30cm2 ( điều cần tìm )
28 tháng 4 2023
S đáy=1/2*8*6=3*8=24cm2
348=2*24+S xq
=>Sxq=300cm2
\(AB=\sqrt{\left(\dfrac{8}{2}\right)^2+\left(\dfrac{6}{2}\right)^2}=5\left(cm\right)\)
\(C_{đáy}=4\cdot5=20\left(cm\right)\)
=>h=300/20=15cm
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............