Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé.
Qua \(C\) vẽ đường thẳng vuông góc với \(CE\) cắt \(AD\) ở \(F\). Kẻ \(BH\perp CD,\) suy ra \(ABHD\) là hình chữ nhật. Do đó \(BH=AD=CD.\) Mặt khác \(\angle CFD=\angle BCH\) (cùng phụ với \(\angle DEC\)). Suy ra \(\Delta CDF=\Delta BHC\) (hai tam giác vuông bằng nhau theo trường hợp g.c.g). Thành thử \(CF=BC.\)
Xét tam giác vuông \(CEF\) có đường cao \(CD\), suy ra \(\frac{1}{CD^2}=\frac{1}{CF^2}+\frac{1}{CE^2}\to\frac{1}{AD^2}=\frac{1}{BC^2}+\frac{1}{CE^2}.\) (ĐPCM).

Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
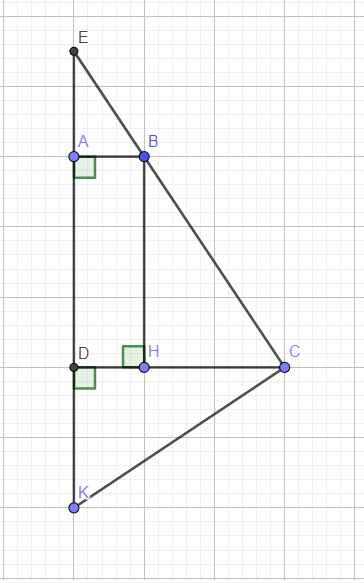
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)
Gái xinh review app chất cho cả nhà đây: https://www.facebook.com/watch/?v=485078328966618 Link tải app: https://www.facebook.com/watch/?v=485078328966618
Kẻ đg cao BH của hình thang ABCD
Qua C kẻ đg thẳng ⊥ với CE cắt AD tại F
+ Tứ giác ABHD là HCN
=> BH = AD = CD
+ ΔBCH = ΔCFD ( g.c.g )
=> BC = CF
+ ΔCEF vuông tại C, đg cao CD
\(\Rightarrow\frac{1}{CD^2}=\frac{1}{CE^2}+\frac{1}{CF^2}\)
\(\Rightarrow\frac{1}{AD^2}=\frac{1}{CE^2}+\frac{1}{BC^2}\)