Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

-Gọi hình thang là ABCD, đáy nhỏ AB, đáy lớn CD, có AC⊥AD.
-Từ đỉnh A kẻ đường cao AH của hình thang. Khi đó, DH = \(\frac{50-14}{2}=18\) (cm) và CH = 50 - 18 = 32 (cm)
-Xét tam giác ACD vuông tại A, đường cao AH có:
\(AH^2=HD.HC=18.32=576\Rightarrow AH=24\)(cm)
-Xét tam giác AHD vuông tại H: \(AD=\sqrt{AH^2+DH^2}=\sqrt{24^2+18^2}=30\) (cm)
-Đã có hết các cạnh và đường cao của hình thang, áp dụng công thức tính ra chu vi và diện tích.

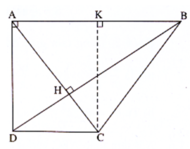
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
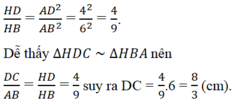
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
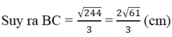
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)

Kẻ CH,DK lần lượt vuông góc AB
ΔCAB vuông tại C
=>CA^2+CB^2=AB^2
=>CA^2+10^2=26^2
=>CA=24cm
ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*26=10*24=240
=>CH=120/13(cm)
ΔCHB vuông tại H
=>HB^2+CH^2=CB^2
=>HB^2=10^2-(120/13)^2=2500/169(cm)
=>HB=50/13(cm)
Xét ΔDKA vuông tại K và ΔCHB vuông tại H có
DA=CB
góc DAK=góc CBH
=>ΔDKA=ΔCHB
=>KA=HB=50/13cm
KH=AB-AK-HB
=26-50/13*2=238/13(cm)
Xét tứ giác KDCH có
DC//KH
DK//CH
Do đó: KDCH là hình bình hành
=>DC=KH=238/13(cm)
S ABCD=1/2*(DC+AB)*CH
=1/2(238/13+26)*120/13
=34560/169(cm2)