Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc OAB=góc ODC
góc OBA=góc BCD
mà góc ODC=góc BCD
nên góc OAB=góc OBA
=>ΔOBA cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
c: ΔABD=ΔBAC
=>góc ABD=góc BAC
=>EA=EB
=>EC=ED
d: OA+AD=OD
OB+BC=OC
mà OA=OB và AD=BC
nên OD=OC
=>OE là trung trực của DC
=>O,E,trung điểm của DC thẳng hàng
a) Chứng minh ΔOAB cân tại O:
Vì AB//CD, ta có ∠ABO = ∠CDO (do là góc đồng quy của hai đường thẳng AB và CD).
Tương tự, vì AB//CD, ta có ∠BAO = ∠DCO (do là góc đồng quy của hai đường thẳng AD và BC).
Do đó, ΔOAB có hai góc bằng nhau với ΔCDO, nên ΔOAB cân tại O.
b) Chứng minh ΔABD = ΔBAC:
Vì AB//CD, ta có ∠ABD = ∠BAC (do là góc đồng quy của hai đường thẳng AB và CD).
Tương tự, vì AB//CD, ta có ∠ADB = ∠CBA (do là góc đồng quy của hai đường thẳng AD và BC).
Do đó, ΔABD có hai góc bằng nhau với ΔBAC, nên ΔABD = ΔBAC.
c) Chứng minh EC = ED:
Vì AC là đường chéo của hình thang ABCD, nên AC chia BD thành hai đoạn bằng nhau.
Do đó, AE = CE và DE = BE.
Vì ΔAEB và ΔCEB có hai cạnh bằng nhau (AE = CE và BE = DE) và góc AEB = góc CEB (do AB//CD), nên ΔAEB = ΔCEB.
Từ đó, ta có EC = ED.
d) Chứng minh O, E và trung điểm của DC thẳng hàng:
Gọi F là trung điểm của DC. Ta cần chứng minh OF//AB.
Vì F là trung điểm của DC, nên DF = FC.
Vì AB//CD, ta có ∠FDC = ∠BAC (do là góc đồng quy của hai đường thẳng AD và BC).
Tương tự, vì AB//CD, ta có ∠FCD = ∠CBA (do là góc đồng quy của hai đường thẳng AD và BC).
Do đó, ΔFDC có hai góc bằng nhau với ΔBAC, nên ΔFDC = ΔBAC.
Từ đó, ta có OF//AB.
Vậy, O, E và trung điểm của DC thẳng hàng.

a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{OCD}=\widehat{ODC}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: Xét ΔACD và ΔBDC có
AC=BD
AD=BC
CD chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
Xét ΔECD có \(\widehat{EDC}=\widehat{ECD}\)
nên ΔECD cân tại E

tu ve hinh nha
CÓ AB//CD
=> GÓC OAB = GOC ODC( 2 GÓC ĐỒNG VỊ )
VA GÓC OBS = GÓC OCD ( 2 GÓC ĐỒNG VỊ )
MÀ GÓC ODC = GÓC OCD( ABCD LÀ HÌNH THANG CÂN )
=> GÓC OAB = GÓC OBÂ
=> TAM GIAC OAB LA TAM GIÁC CÂN
B) XÉT TAM GIÁC BAD VÀ TAM GIÁC ABC CÓ :
AD=BC( ABCD LÀ HÌNH THANG CÂN )
AB CHUNG
AC=DC ( ABCD LA HINH THANG CÂN )
=> Tam giác ABD = tgiac BAC
C) CÓ TAM GIÁC ABC= TAM GIÁC BAD( CM CÂU B)
=> GÓC BAC = GÓC ABD ( 2 GÓC TƯƠNG ỨNG )
=> TAM GIÁC EAB CÂN TẠI E( CMT CÂU C)
=> AE=BE( ĐN TAM GIÁC CÂN )
CÓ AC = BD( ABCD LÀ HÌNH THANG CÂN )
MÀ AE = BE ( CMT)
=> ED=EC
D) CÓ AO =BO( TAM GIÁC AOB CÂN TẠI O)
=> O THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
CÓ EB=EB
=> E THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
=> OE THUỘC VÀO ĐG TT CỦA AB
CÓ OD=OC ( CÁI NÀY TỰ CM )
=> O THUỘC VÀO ĐG TT CỦA CD
CÓ ED=EC
=> E THUỘC VÀO ĐG TT CỦA CD
=> OE THUỘC ....... CD

Ta có : ABCD là hình thang cân
\(\Rightarrow C=D\)(góc đáy hình thang cân)
\(\Rightarrow\)Tam giác EDC là tam giác cân tại E.
Vì : góc A = góc D
Ta lại có : M trung điểm của DC
\(\Rightarrow\) : EM vuông góc với DC ( tam giác EDC cân )
Hay EM là đường cao của tam giác EDC
Mà : O là giao điểm của AC và DB
Nên : EM sẽ đi qua O
Vậy : E,O,M thẳng hàng (đpcm)

a) Vì ABCD là hình thang cân
=> AD = BC
=> ADC = BCD
=> AC = BD
=> DAB = CBA
Xét ∆ADC và ∆BCD ta có :
AD = BC
ADC = BCD
DC chung
=> ∆ADC = ∆BCD (c.g.c)
=> BDC = ACD ( tương ứng)
=> ∆DOC cân tại O.
b) Mà DAB + BAE = 180° ( kề bù)
ABC + ABE = 180° ( kề bù )
Mà DAB = CBA
=> EAB = EBA
=> ∆EAB cân tại E
Gọi giao điểm AB và EO là H
EO và DC là G
Mà AB//CD
=> BAC = ACD ( so le trong)
=> ABD = ACD ( so le trong)
Mà ACD = BDC
=> CAB = ABD
=> ∆ABO cân tại O
=> EO là trung trực và là phân giác ∆AOB
=> AOH = BOH ( phân giác )
Mà AOH = COG ( đối đỉnh)
BOH = DOG ( đối đỉnh)
Mà AOH = BOH ( EO là phân giác)
=> OG là phân giác DOC
Mà ∆DOC cân tại O
=> OG là trung trực DC
Hay EO là trung trực DC
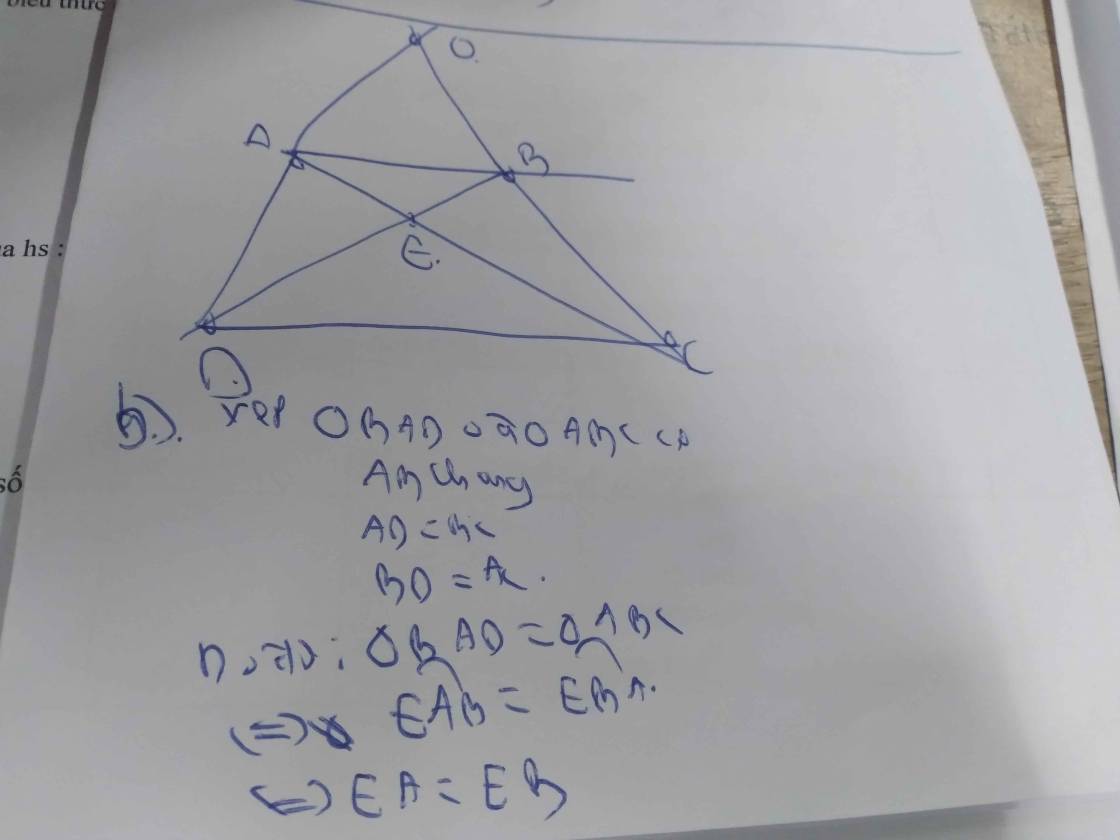

Bổ sung đề : ABCD là hthang cân
a) Ta có:
ABCD là hthang cân
=> \(\widehat{BAD}=\widehat{ABC}\)
\(\Rightarrow180^0-\widehat{BAD}=180^0-\widehat{ABC}\)
\(\Rightarrow\widehat{OAB}=\widehat{OBA}\)
=> Tam giác AOB cân tại O
b) Xét ΔABD và ΔBAC có:
AD=BC(ABCD là hthang cân)
\(\widehat{BAD}=\widehat{ABC}\)(ABCD là hthang cân)
AB chung
=> ΔABD=ΔBAC(c.g.c)
c) Ta có: ΔABD=ΔBAC(cmt)
=> \(\widehat{EDC}=\widehat{ECD}\)
=> Tam giác EDC cân tại E
=>EC=ED
e cảm ơn nhiều lắm ạ❤