Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tu ve hinh nha
CÓ AB//CD
=> GÓC OAB = GOC ODC( 2 GÓC ĐỒNG VỊ )
VA GÓC OBS = GÓC OCD ( 2 GÓC ĐỒNG VỊ )
MÀ GÓC ODC = GÓC OCD( ABCD LÀ HÌNH THANG CÂN )
=> GÓC OAB = GÓC OBÂ
=> TAM GIAC OAB LA TAM GIÁC CÂN
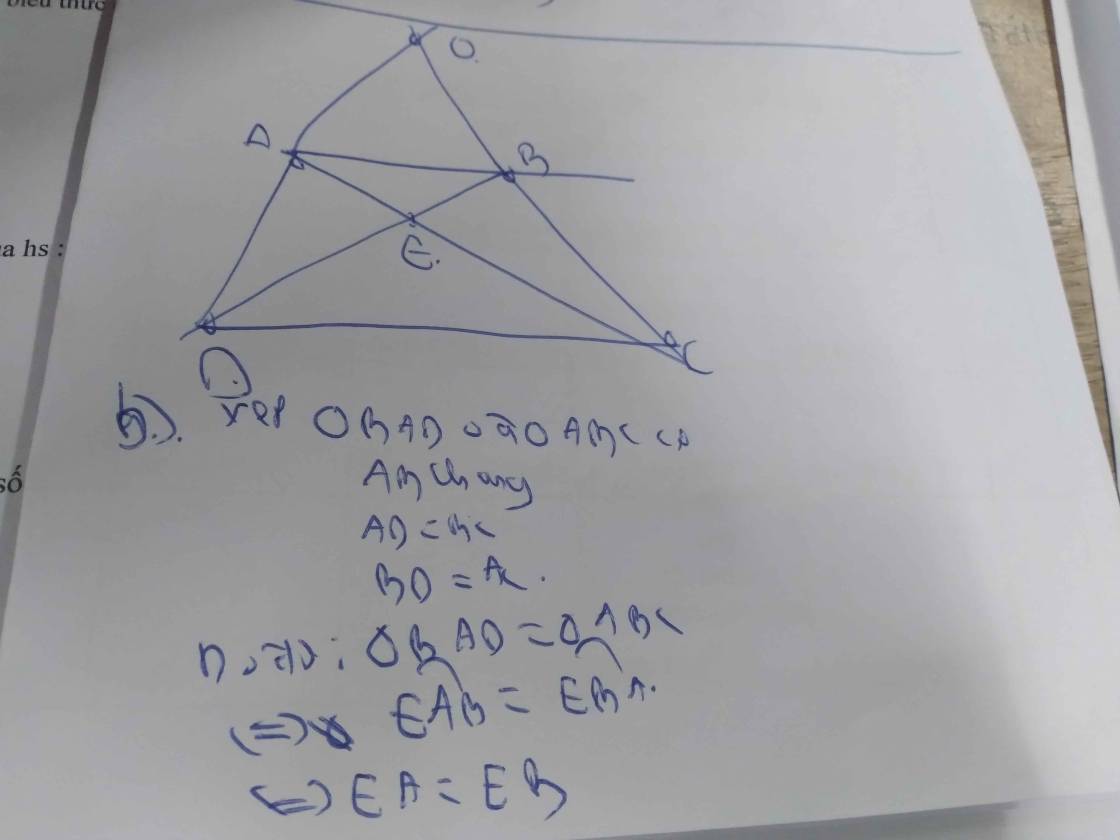
B) XÉT TAM GIÁC BAD VÀ TAM GIÁC ABC CÓ :
AD=BC( ABCD LÀ HÌNH THANG CÂN )
AB CHUNG
AC=DC ( ABCD LA HINH THANG CÂN )
=> Tam giác ABD = tgiac BAC
C) CÓ TAM GIÁC ABC= TAM GIÁC BAD( CM CÂU B)
=> GÓC BAC = GÓC ABD ( 2 GÓC TƯƠNG ỨNG )
=> TAM GIÁC EAB CÂN TẠI E( CMT CÂU C)
=> AE=BE( ĐN TAM GIÁC CÂN )
CÓ AC = BD( ABCD LÀ HÌNH THANG CÂN )
MÀ AE = BE ( CMT)
=> ED=EC
D) CÓ AO =BO( TAM GIÁC AOB CÂN TẠI O)
=> O THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
CÓ EB=EB
=> E THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
=> OE THUỘC VÀO ĐG TT CỦA AB
CÓ OD=OC ( CÁI NÀY TỰ CM )
=> O THUỘC VÀO ĐG TT CỦA CD
CÓ ED=EC
=> E THUỘC VÀO ĐG TT CỦA CD
=> OE THUỘC ....... CD

a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{OCD}=\widehat{ODC}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: Xét ΔACD và ΔBDC có
AC=BD
AD=BC
CD chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
Xét ΔECD có \(\widehat{EDC}=\widehat{ECD}\)
nên ΔECD cân tại E

Trần Đăng Khang tham khảo nhé:
Tứ giác ABCD là hình thang nên:AB//CD.
Gọi M, N lần lượt là giao điểm của KO với AB,CD.
Áp dụng định lý talet ta có:
AM/DN=MB/NC(=KM/KN)
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC.
=AO/OC=AM/NC.
Vậy AM/DN=AM/NC hay DN=NC.
tương tự MB=MA.
hay ta có OK đi qua trung điểm của AB và CD.

Tham khảo a làm rồi nha: https://hoc24.vn/cau-hoi/.1904701261424