Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

. Vẽ đường cao BH xuống AC, đường cao DI xuống AC : có S(ABC) = 2/3 S(ADC) (chung chiều cao hình thang, đáy AB = 2/3 DC) .
Mà hai tam giác này có chung đáy AC nên chiều cao BH = 2/3 DI.
Xét trong tam giác ABE và ADE có: chung đáy AE, chiều cao BH = 2/3 DI.
-> S (ABE) = 2/3 S (ADE)
-> S(ADE) = 4X3/2 = 6 cm2
b. Diện tích ADC=3/2ABC ví DC=3/2AB,cùng chjều cao hình thang.
Gọi chiều cao hạ từ D và B đến AC là H và L.
DH=3/2BL vì chung đáy AC và diện tích ADC=3/2ABC.
Diện tích ADC=BDC vì chung đáy DC và chiều cao bằng nhau. Hai tam giác này có chung tam giác DEC nên diện tích AED=EBC.
AE=2/3EC vì diện tích AEB=EBC,DH=3/2BL.
Diện tích BEC=3/2ABE=3X4:2=6 cm vuôngvì chung chjều cao, AE=2/3EC.
Vậy SADE bằng 6cm2. Câu a ta đã chứng minh AE=2/3EC

A B C D O
a/
Hai tg ABD và tg ABC có chung AB và đường cao từ D->AB = đường cao từ C->AB nên \(S_{ABD}=S_{ABC}\)
Hai tg này có phần diện tích chung là \(S_{ABO}\Rightarrow S_{AOD}=S_{BOC}\)
b/
Hai tg ABC và tg ACD có đg cao từ D->AB = đường cao từ B->CD nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{1}{2}\)
Hai tg trên có chung AC nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\) đg cao từ B->AC / đg cao từ D->AC\(=\dfrac{1}{2}\)
Hai tg ABO và tg AOD có chung AO nên
\(\dfrac{S_{ABO}}{S_{AOD}}=\) đg cao từ B->AC / đg cao từ D->AC\(=\dfrac{1}{2}\)
\(\Rightarrow S_{AOD}=2xS_{ABO}=2x3,5=7cm^2\)
\(\Rightarrow S_{ABD}=S_{ABO}+S_{AOD}=3,5+7=10,5cm^2\)
Hai tg ABD và tg BCD có đg cao từ D->AB = đường cao từ B->CD nên
\(\dfrac{S_{ABD}}{S_{BCD}}=\dfrac{AB}{CD}=\dfrac{1}{2}\Rightarrow S_{BCD}=2xS_{ABD}=2x10,5=21cm^2\)
\(\Rightarrow S_{ABCD}=S_{ABD}+S_{BCD}=10,5+21=31,5cm^2\)
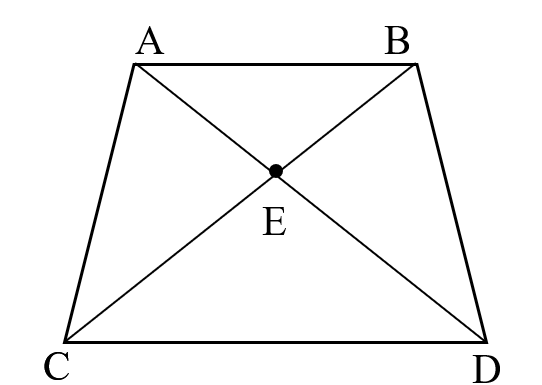
a. Vẽ đường cao BH xuống AC, đường cao DI xuống AC : có S(ABC) = 2/3 S(ADC) (chung chiều cao hình thang, đáy AB = 2/3 DC) . Mà hai tam giác này có chung đáy AC nên chiều cao BH = 2/3 DI. Xét trong tam giác ABE và ADE có: chung đáy AE, chiều cao BH = 2/3 DI. -> S (ABE) = 2/3 S (ADE) -> S(ADE) = 4X3/2 = 6 cm2 b. Diện tích ADC=3/2ABC ví DC=3/2AB,cùng chjều cao hình thang. Gọi chiều cao hạ từ D và B đến AC là H và L. DH=3/2BL vì chung đáy AC và diện tích ADC=3/2ABC. Diện tích ADC=BDC vì chung đáy DC và chiều cao bằng nhau. Hai tam giác này có chung tam giác DEC nên diện tích AED=EBC. AE=2/3EC vì diện tích AEB=EBC,DH=3/2BL. Diện tích BEC=3/2ABE=3X4:2=6 cm vuôngvì chung chjều cao, AE=2/3EC. Vậy SADE bằng 6cm2. Câu a ta đã chứng minh AE=2/3EC