Question

[8/5_06 Trương Võ Đức Duy]

Cho hình thang ABCD có hai đấy là AB và CD, M là trung điểm của AB, O là giao điểm của AD và BC. OM cắt CD tại N. Chứng minh N là trung điểm của CD

Answer 1

[Dr.STONE]

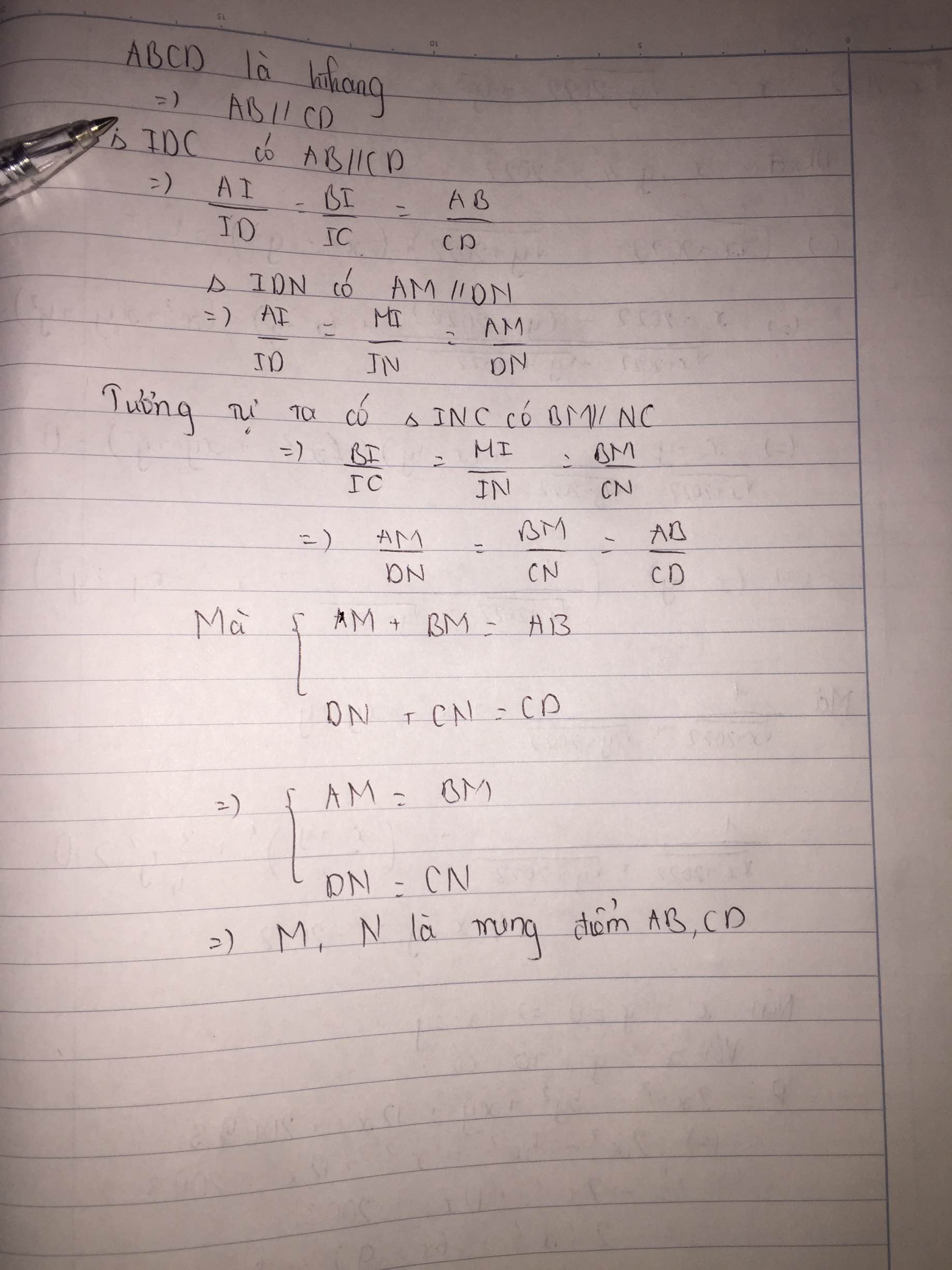
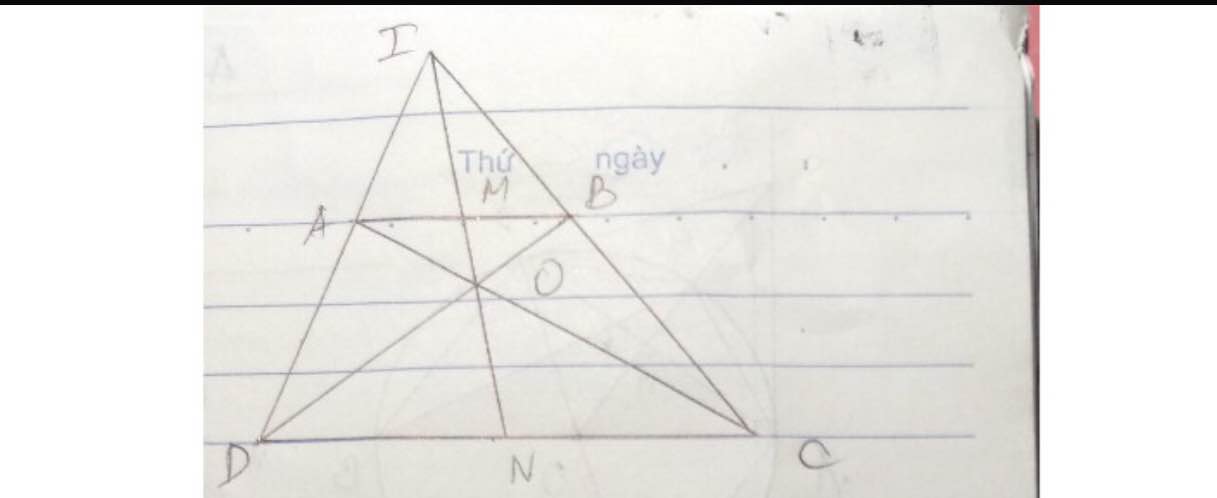
- Xét tam giác ODN có: AM//DN.

=>\(\dfrac{AM}{DN}=\dfrac{OM}{ON}\)(định lí Ta-let) (1)

- Xét tam giác OCN có: BM//CN.

=>\(\dfrac{BM}{CN}=\dfrac{OM}{ON}\)(định lí Ta-let) (2)

- Từ (1) và (2) suy ra \(\dfrac{AM}{DN}=\dfrac{BM}{CN}\)mà AM=BM (M là trung điểm AB)

Nên DN=CN. Vậy N là trung điểm của CD.

Answer 2

[8/5_06 Trương Võ Đức Duy]

Vẽ hình luôn giúp tớ được không!!