Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự tìm
b) Sử dụng các cặp góc so le trong của hai đường thẳng song song và tính chất tia phân giác.
c) Suy ra từ b)
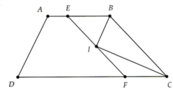

em tự vẽ hình
câu 1 em tự chứng minh nhé
câu 2,
ta có IE//BC\(\Rightarrow\widehat{EIC}=\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}=\widehat{ICB}\) (phân giác )
=> \(\widehat{EIC}=\widehat{ECI}\)
=> tam giác IEC cân tại E
chứng minh tương tự cvới tam giác kia nhé
c)
ta có tam giác IEC cân tại E=> IE=EC
vơi tam giác kia cân thì ta có IF=FB
=> IE+IF=BF+CE
=> EF=BF+IC

a) Xét tam giác ACD có: AF=FC (gt) ; DK=KC (gt)
=> FK là đường trung bình của tam giác ACD
=> FK//AD
=> ADKF là hình thang
Chứng minh tương tự t cũng có: ME là đường trung bình của tam giác ABD
=> ME // AD mà FK//AD (cmt)
=> ME//FK (1)
Chứng minh tương tự ta cũng có:
MF là đường trung bình tam giác ABC , EK là đường trung bình tam giác DBC
=> MF//BC ; EK // BC
=> MF//EK (2)
Từ (1) và (2) ta có: EMFK là hình bình hành

a) Xét tam giác ABC và tam giác BAD, ta có:
AB: cạnh chung
AC=AD (ABCD:hình thang cân)
BC=AD (ABCD: hình thang cân)
=>Tam giác ABC = tam giác BAD (c-c-c)
=>\(\widehat{ACB}\)=\(\widehat{BDA}\)(2 góc t/ứng)
Ta có:
\(\widehat{ACD=}\widehat{ACB}\)+\(\widehat{BCD}\)
BDC^ = BDA^ + ADC^
ACD^ = BDC^ (ABCD: hình thang cân)
ACB^ = BDA^ (cmt)
=>BCD^ = ADC^
Ta lại có AB//CD (gt):
=> ABC^ = BCD^ (2 góc sole trong)
BAD^ = ADC^ (2 góc sole trong)
BCD^ = ADC^ (cmt)
=> ABC^ = BAD^
Ta có ME//BC (gt):
=> MEA^ = ABC^ (2 góc sole trong)
Mà ABC^ = BAD^ (cmt)
=> MEA^ = BAD^
Mặt khác: MAE^ = BAD^ ( 2 góc đối đỉnh)
=> MEA^ = MAE^
=> Tam giác MAE cân tại M.
MIK xin lỗi, mik đánh sai đề bài, sửa lại như sau:
a) Tam giác MAE cân
b) AF = DE
\(a,\) Ta có \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right);\widehat{B_2}=\widehat{I_1}\left(so.le.trong.do.EI//BC\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta BEI.cân.tại.E\)
Ta có \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right);\widehat{C_2}=\widehat{I_2}\left(so.le.trong.do.FI//BC\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{I_1}\Rightarrow\Delta CFI.cân.tại.F\)
\(b,\) Vì \(\Delta BEI.và.\Delta CFI\) cân nên \(\left\{{}\begin{matrix}BE=EI\\CF=FI\end{matrix}\right.\)
\(\Rightarrow BE+CF=EI+FI=EF\)
Các hình thang: BEFC do EF//BC; ADFE do AE//DF; ABCD do giả thiết