Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KB/KM=AB/CM=AB/MD
Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD
=>IA/IM=KB/KM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔADM có EI//DM
nên EI/DM=AI/AM
=>EI/CM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên IK/AB=MK/MB=MI/MA
=>BK/BM=AI/AM
=>EI/DM=KF/DM
=>EI=KF
c: Xét ΔOAN và ΔOCM có
góc OAN=góc OCM
góc AON=góc COM
=>ΔOAN đồng dạng với ΔOCM
=>OA/OC=AN/CM
Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOb=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=AB/CD
=>AB/CD=AN/CM
=>AB/AN=CD/CM=2
=>AB=2AN
=>N là trung điểm của AB

ĐỪNG ẤN ĐỌC THÊM
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Đã kêu đừng ấn mà đéo nghe :))))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Thôi, lướt tiếp đi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Lần này nữa thôi :)))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Cố lên
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.

a: Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>AB/MD=IA/IM=AB/MC
Xet ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=.ΔKAB đồng dạng với ΔKCM
=>AB/KC=KB/KC
=>KB/KC=IA/IM
=>IK//AB
b: Xét ΔAMD có IE//MD
nên IE/MD=AE/AD=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BF/BC
=>IE/MD=KF/MC
=>IE=KF
IK//AB
=>IK/AB=MI/MA
=>\(IK=AB\cdot\dfrac{MI}{MA}=MD\cdot\dfrac{IA}{IM}\cdot\dfrac{MI}{MA}=MD\cdot\dfrac{IA}{MA}\)
\(=\dfrac{1}{2}\cdot CD\cdot\dfrac{IA}{MA}\)
IE/DM=AI/AM
=>\(IE=\dfrac{1}{2}\cdot CD\cdot\dfrac{AI}{AM}\)
=>IE=IK=KF
c: \(CD+AB=45\cdot2:6=90:6=15\left(cm\right)\)
CD=2/3*15=10cm
AB=15-10=5cm

Ban có đáp án câu này chưa cho mình xin với. Mình cũng đang học
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

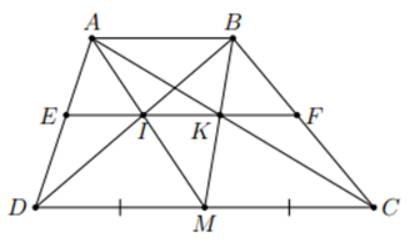
a) Vì AB // CD áp dụng định lý Ta-lét ta có:
\(\dfrac{IM}{IA}\)=\(\dfrac{MD}{AB}\)
\(\Rightarrow\) \(\dfrac{IM}{IA}\)=\(\dfrac{KM}{KB}\) (Vì MC = MD)
\(\dfrac{KM}{KB}\)=\(\dfrac{MC}{AB}\)
Do đó theo định lý Ta-lét đảo ta có IK // AB
Vì IK // AB // CD nên theo định lý Ta-lét :
\(\dfrac{IE}{DM}\)=\(\dfrac{AI}{AM}\)=\(\dfrac{BI}{BD}\)=\(\dfrac{IK}{DM}\)=> EI = IK
Tương tự ta có FK =IK nên ta có EI = IK = KF

Ta có: AB//CD => AB//DM
=> \(\frac{AI}{IM}=\frac{AB}{DM}\)
AB// MC
=> \(\frac{BK}{KM}=\frac{AB}{MC}\)
Mà DM=MC
=> \(\frac{AI}{IM}=\frac{BK}{KM}\)=> IK//AB
b) IK//AB
=> EI//DM => \(\frac{EI}{DM}=\frac{AI}{AM}\)
IK//MC => \(\frac{AI}{AM}=\frac{IK}{MC}=\frac{BK}{BM}\)
KF//MC => \(\frac{BK}{BM}=\frac{KF}{MC}\)
=> \(\frac{EI}{DM}=\frac{IK}{MC}=\frac{KF}{MC}\)Mà DM =MC
=> EI=IK=KF

a) Do \(AB//DC\Rightarrow AB//DM\) \(\Rightarrow\frac{AB}{DM}=\frac{AI}{IM}\)( Talet ) (1)
Tương tự ta có : \(\frac{AB}{CM}=\frac{BK}{KM}\) ( Talet ) (2)
Lại có : \(DM=CM\left(gt\right)\) nên từ (1) và (2)
\(\Rightarrow\frac{AI}{IM}=\frac{BK}{KM}\)
Xét \(\Delta ABM\) có \(\frac{AI}{IM}=\frac{BK}{KM}\) (cmt) , \(I\in AM,K\in BM\)
\(\Rightarrow IK//AB\) ( định lý Talet đảo )
b) Áp dụng định lý Talet lần lượt ta được :
+) \(EI//DM\Rightarrow\frac{EI}{DM}=\frac{AI}{AM}\) (3)
+) \(IK//MC\Rightarrow\frac{AI}{AM}=\frac{AK}{AC}=\frac{IK}{MC}\)(4)
+) \(KF//MC\Rightarrow\frac{BK}{BM}=\frac{KF}{MC}\) (5)
Mà : \(DM=CM\left(gt\right)\)
Nên tuqd (3) (4) và (5) \(\Rightarrow EI=IK=KF\) (đpcm)
a ) Hướng giải :
- Cần chứng minh tứ giác ABDM và tứ giác ABMC là hình bình hành.
- Suy ra KM // AD và IM // BC
- Áp dụng tính chất đường trung bình vào 2 tam giác ADC và DBC
- IK là đường trung bình của tam giác ABM
- IK // AB // DC
b ) Hướng giải ;
- Đầu tiên, cần chứng minh 4 điểm E, I, K, F thẳng hàng theo Tiên đề Ơ - clit
- Tiếp tục dùng tính chất đường trung bình vào các tam giác ADM, BMC
- Cuối cùng, EI = IK = KF \(\left(=\frac{DM}{2}=\frac{MC}{2}\right)\)

a: Xét ΔEAB và ΔECM có
\(\widehat{EAB}=\widehat{ECM}\)(hai góc so le trong, AB//CM)
\(\widehat{AEB}=\widehat{CEM}\)(hai góc đối đỉnh)
Do đó: ΔEAB đồng dạng với ΔECM
=>\(\dfrac{EA}{EC}=\dfrac{EB}{EM}=\dfrac{AB}{CM}\)
=>\(\dfrac{EA}{EC}=\dfrac{AB}{CM}=AB:\dfrac{CD}{2}=2\cdot\dfrac{BA}{CD}\)
b: Xét ΔFAB và ΔFMD có
\(\widehat{FAB}=\widehat{FMD}\)(hai góc so le trong, AB//DM)
\(\widehat{AFB}=\widehat{MFD}\)(hai góc đối đỉnh)
Do đó: ΔFAB đồng dạng với ΔFMD
=>\(\dfrac{FA}{FM}=\dfrac{FB}{FD}=\dfrac{AB}{MD}\)
Ta có: \(\dfrac{FA}{FM}=\dfrac{AB}{MD}\)
\(\dfrac{EB}{EM}=\dfrac{AB}{CM}\)
mà MD=MC
nên \(\dfrac{FA}{FM}=\dfrac{EB}{EM}\)
=>\(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
Xét ΔMAB có \(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
nên FE//AB
Ta có: FE//AB
AB//CD
Do đó: FE//CD
c: Xét ΔADM có HF//DM
nên \(\dfrac{HF}{DM}=\dfrac{AF}{AM}\)
Xét ΔBDM có FE//DM
nên \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
Xét ΔBMC có EG//MC
nên \(\dfrac{EG}{MC}=\dfrac{BE}{BM}\)
mà \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
và MC=MD
nên FE=EG
Ta có: \(\dfrac{AF}{FM}=\dfrac{BE}{EM}\)
=>\(\dfrac{FM}{FA}=\dfrac{EM}{BE}\)
=>\(\dfrac{FM}{FA}+1=\dfrac{EM}{BE}+1\)
=>\(\dfrac{FM+FA}{FA}=\dfrac{EM+BE}{BE}\)
=>\(\dfrac{AM}{FA}=\dfrac{BM}{BE}\)
=>\(\dfrac{AF}{AM}=\dfrac{BE}{BM}\)
mà \(\dfrac{HF}{DM}=\dfrac{AF}{AM}\) và \(\dfrac{BE}{BM}=\dfrac{FE}{DM}\)
nên HF=FE
mà FE=EG
nên HF=FE=EG
a. -Xét △ABH có: AB//DM (gt)
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{DM}\) (định lí Ta-let)
Mà \(DM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
b. Sửa đề: C/m HK//AB.
-Xét △ABK có: AB//CM (gt)
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{CM}\) (định lí Ta-let)
Mà \(CM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
-Xét △ABM có: \(\dfrac{AH}{HM}=\dfrac{AK}{KC}\left(=\dfrac{2AB}{CD}\right)\)
\(\Rightarrow\)HK//AB.
c. -Xét △ABM có: HK//AB (cmt).
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{AM}{HM}\) (định lí Ta-let).
\(\Rightarrow\dfrac{AB-HK}{HK}=\dfrac{AM-HM}{HM}\)
\(\Rightarrow\dfrac{AB}{HK}-1=\dfrac{AH}{HM}\)
Mà \(\dfrac{AH}{HM}=\dfrac{2AB}{CD}\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{2AB}{CD}\)
\(\Rightarrow\dfrac{a}{HK}=\dfrac{2a}{b}\)
\(\Rightarrow HK=\dfrac{b}{a}\)