Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ đường cao MK
\(S_{MNA}=\dfrac{1}{2}\cdot MK\cdot NA\)
\(S_{MNP}=\dfrac{1}{2}\cdot MK\cdot NP\)
=>\(\dfrac{S_{MNA}}{S_{MNP}}=\dfrac{NA}{NP}=\dfrac{2}{3}\)
b: \(S_{MNA}=\dfrac{2}{3}\cdot S_{MNP}\)
=>\(S_{MAP}=\dfrac{1}{3}\cdot S_{MNP}=\dfrac{1}{3}\cdot36=12\left(cm^2\right)\)

Đáp án+Giải thích các bước giải:
Bài giải
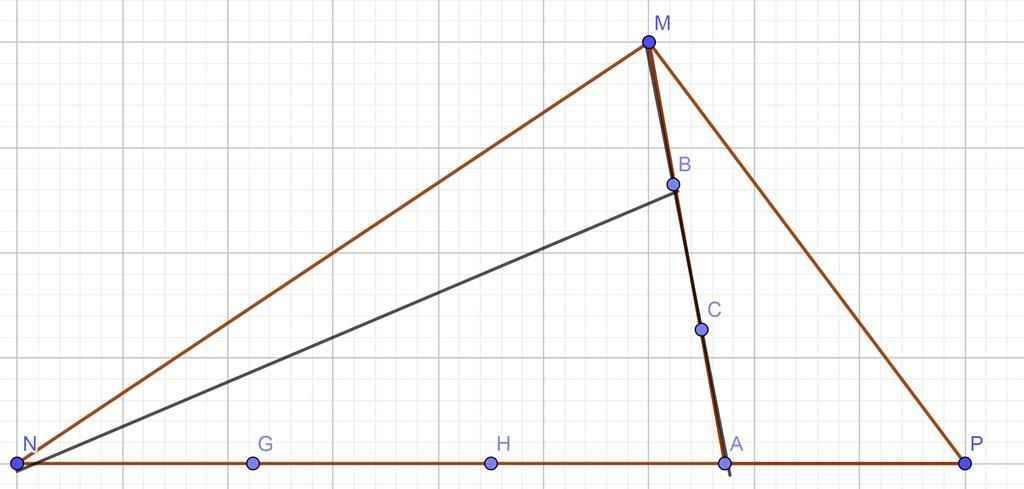
Ta có hình vẽ:
Nhìn vào hình, ta thấy S HTG MPN được chia thành 4 hình TG có S = nhau vì đáy của chúng (NG,GH,HA,AP) đều = 1/4 đáy HTG MPN và có cùng chiều cao.
Nếu trong HTG MPN bớt đi HTG MPA thì còn lại là HTG MNA. Như trên hình, HTG MNA được chia thành 3 hình TG theo chiều dọc cũng có đáy và chiều cao = nhau. Tương tự chia theo chiều ngang thì cũng được 3 HTG có S = nhau như vậy. Mà S HTG MNB = 13cm2 nên S 2 HTG còn lại trong hình TG MNA cũng bằng 13cm2, chia theo chiều dọc ta cũng được S như vậy . S 1 trong 3 HTG trong HTG MNA = 13cm2 mà S 1 HTG trong đó = S HTG MPA nên S HTG MPA cũng = 13cm2.
Cả HTG MPN được chia thành 4 HTG có S = nhau.
S HTG MPN là:
13 * 4 = 52 (cm2)
Đáp số : 52 cm2
Hình ảnh:

Hai tg AMC và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow S_{AMC}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMN và tg AMC có chung đường cao từ A->CM nên
\(\dfrac{S_{AMN}}{S_{AMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{AMN}=\dfrac{1}{2}xS_{AMC}=\dfrac{1}{2}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{6}xS_{ABC}\)
\(S_{BMC}=S_{ABC}-S_{AMC}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
Hai tg BMN và tg BMC có chung đường cao từ B->MC nên
\(\dfrac{S_{BMN}}{S_{BMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{BMN}=\dfrac{1}{2}xS_{BMC}=\dfrac{1}{2}x\dfrac{2}{3}xS_{ABC}=\dfrac{1}{3}xS_{ABC}\)
\(S_{ANB}=S_{AMN}+S_{BMN}=\dfrac{1}{6}xS_{ABC}+\dfrac{1}{3}xS_{ABC}=\dfrac{1}{2}xS_{ABC}=40cm^2\)
Gọi $S_{MNB}$ là diện tích tam giác $MNB$, $x$ là diện tích tam giác $MPN$.
Ta có $MB = CA$, suy ra $S_{MNB} = S_{MCA}$.
Gọi $h$ là độ cao của tam giác $MPN$ từ đỉnh $P$. Ta có:
$$\frac{AP}{AN} = \frac{1}{3} \Rightarrow \frac{PN}{AN} = \frac{2}{3} \Rightarrow \frac{h}{MA} = \frac{2}{3} \Rightarrow h = \frac{2}{3} MA$$
Do $MB = CA$, suy ra $S_{MNB} = S_{MCA} = \frac{1}{2} MB \cdot h = \frac{1}{2} CA \cdot h$.
Mà $MB + CA = MA$, suy ra $S_{MNB} + S_{MCA} = \frac{1}{2} MA \cdot h$.
Từ đó, ta có:
$$2S_{MNB} = \frac{1}{2} MA \cdot h - S_{MNB} = \frac{1}{2} S_{MPN}$$
$$\Rightarrow S_{MPN} = 4S_{MNB} = 4 \cdot 13 = 52 \text{ (cm}^2\text{)}$$
Vậy diện tích tam giác $MPN$ là 52 cm$^2$.