Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

Đáp án A
Phương pháp: Công thức tính diện tích xung quanh của hình nón: S x q = π R l
Cách giải:

Có: l = 2 R 2 = a 2 2
S x q = π R l = π . a 2 . a 2 2 = π a 2 2 4
Chú ý khi giải: HS thường nhầm lẫn công thức tính diện tích xung quanh hình nón là S x q = π R h với h là đường cao của hình nón.

Đáp án C
Phương pháp: Diện tích xung quanh của hình nón: S x q = π R l
Trong đó : R bán kính đáy, l độ dài đường sinh.
Cách giải: Tam giác ABC vuông cân tại A, AH ⊥ BC
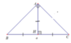
=> AH = HB = HC

Diện tích xung quanh của hình nón:
S x q = π R l
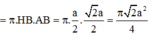

Đáp án D
Δ S A B vuông cân tại S , A B = 4 a
⇒ S A = S B = 4 a 2 = 2 a 2
⇒ l = 2 a 2
Δ S A C cân tại S , A S C ^ = 120 0
⇒ S A C ^ = S C A ^ = 30 0
⇒ c o s S A O ^ = O A S A hay 3 2 = R 2 a 2 ⇒ R = a 6
S x q = π R l = π . a 6 .2 a 2 = π 4 a 2 3 .

Đáp án D.
Gọi thiết diện qua trục là tam giác cân SAB có S A = 2 A B .
Ta có:
S O 2 = S A 2 − A O 2 = 4 A B 2 − O A 2 = 15 r 2 = h 2 ⇒ r = 15 5 c m .
Diện tích xung quanh của hình nón là: S x q = π r l = π r h 2 + r 2 = 12 5 c m 2 .

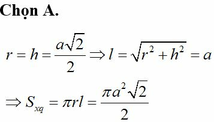
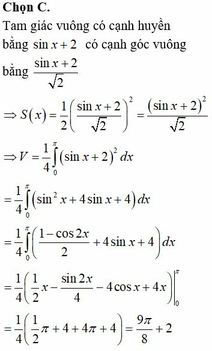

Đáp án A