

![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


![]()

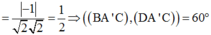

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

\(OB=\sqrt{SB^2-SO^2}=\frac{a\sqrt{3}}{3}\) \(\Rightarrow OA=\sqrt{AB^2-OB^2}=\frac{a\sqrt{6}}{3}\)
Đặt hệ trục Oxyz vào hình chóp với \(Oz\) trùng tia \(OS\); \(Ox\) trùng tia OB, Oy trùng tia OA, \(\frac{a}{3}\) bằng 1 đơn vị độ dài
\(\Rightarrow S\left(0;0;\sqrt{6}\right)\); \(A\left(0;\sqrt{6};0\right);B\left(\sqrt{3};0;0\right);D\left(-\sqrt{3};0;0\right)\)
\(\Rightarrow\overrightarrow{SA}=\left(0;\sqrt{6};-\sqrt{6}\right)=\sqrt{6}\left(0;1;-1\right)\)
\(\overrightarrow{SB}=\left(\sqrt{3};0;-\sqrt{6}\right)=\sqrt{3}\left(1;0;-\sqrt{2}\right)\)
\(\overrightarrow{SD}=\left(-\sqrt{3};0;-\sqrt{6}\right)=-\sqrt{3}\left(1;0;\sqrt{2}\right)\)
\(\Rightarrow\overrightarrow{n_{\left(SAB\right)}}=\left[\overrightarrow{SA};\overrightarrow{SB}\right]=\left(\sqrt{2};1;1\right)\)
\(\overrightarrow{n_{\left(SAD\right)}}=\left[\overrightarrow{SA};\overrightarrow{SD}\right]=\left(\sqrt{2};-1;-1\right)\)
\(\Rightarrow cos\alpha=\frac{\left|2-1-1\right|}{\sqrt{2+1+1}\sqrt{2+1+1}}=0\Rightarrow\alpha=90^0\)

Chọn đáp án C.
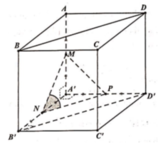
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa ![]()
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên ![]()
Suy ra 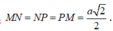
Do đó tam giác MNP đều ![]()