K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

21 tháng 6 2016
\(\begin{cases}\left(SBC\right)\perp\left(ABCD\right)\\SH\perp CB\\\left(SBC\right)\cap\left(ABCD\right)=AB\end{cases}\Rightarrow SH\perp\left(ABCD\right)}\)

NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)
 A.3a3 B.a3 C.a3
A.3a3 B.a3 C.a3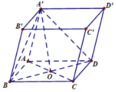
ta có BI=\( \frac{2a}{3}\).nhận thấy góc giữa hai mp(B\(B^,C^,C\)) và đáy là góc giữa hai đường thẳng \(BB^,\) vàAB =30\(^o \)
Xét tam giác \(BB^,I\) vông tại I có:
tan(30)=\(\frac{B^, I}{IB}\)=\(\frac{h}{\frac{2a}{3}}\) →h=\(\frac{2\sqrt{3}a}{9}\) từ đó suy ra thể tích V=h.S=\(\frac{2\sqrt{3}a^3}{9}\)
thaks ban nha. hj