Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho hình hộp ABCD.A'B'C'D' có các cạnh đều =a. góc BAD =60•, BAB' =DAD'=120•.tính góc giữa đường thẳng AB và A'D',AC',B'D.tính diện tích A'B'CD và A'CC'A'

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

Áp dụng định lý Pitago cho tam giác vuông ABC
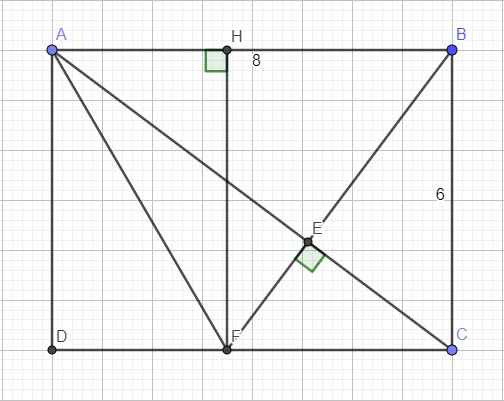
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)

a) Ta có \(\widehat{BOM}=sđ\stackrel\frown{BM}\) (đ/lí góc ở tâm)
Mà \(\stackrel\frown{BM}=120^o=>\widehat{BOM}=120^o\)
Vì \(\widehat{BOM}+\widehat{AOM}=180^o=>\widehat{AOM}=60^o\)
Xét \(\Delta AOM\) có
OA = OM (bán kính)
\(\widehat{AOM}=60^o\left(cmt\right)\)
\(=>\Delta OAM\) đều (dhnb tam giác đều)
b) +) Ta có \(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
mà \(\Delta OAM\) đều (cmt) \(=>\widehat{OAM}=60^o\)
\(=>\widehat{ABM}=30^o\)
+) Vì R = 3 cm (gt) => OA = OB = 3 cm => AB = 6cm
Xét \(\Delta AMB\) vg tại A
\(=>AB^2=AM^2+BM^2\)
\(=>6^2=3^2+BM^2\)
\(=>BM=3\sqrt{3}\)

Bài 1:
a: \(AB=21\cdot\dfrac{3}{7}=9\left(cm\right)\)
AC=21-9=12(cm)
=>BC=15(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=7,2(cm)
Xét ΔAHB vuông tại H có \(AB^2=AH^2+BH^2\)
hay BH=5,4(cm)
=>CH=9,6(cm)