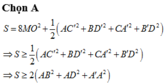Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
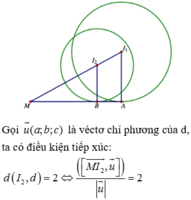
Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có S O ⊥ A B C .
Do A E ⊥ B C S O ⊥ B C ⇒ B C ⊥ ( S A E ) .
Dựng E K ⊥ S A suy ra EK là đoạn vuông góc chung cua SA và BC.
Tương tự dựng FI; RL là các đoạn vuông góc chung cùa 2 cạnh đoi diện. Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M. Như vậy d ≥ K + F I + R L = 3 E K
Mặt khác K E = a 3 2 ⇒ cos S A O ^ = 1 3 ⇒ s i n S A O ^ = 2 2 3
Do đó K E = A E . sin A = a 3 2 . a 2 3 = a 6 3
Do vậy d m i n = a 6 .

Đáp án C
Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có: S O ⊥ A B C
Do A E = B C S O = B C ⇒ B C ⊥ S A E . Dựng E K ⊥ A suy ra EK là đoạn vuông góc cung của SA và BC. Tương tự dựng FI; RL là các đoạn vuông góc chung của 2 cạnh đối diện.
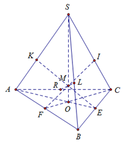
Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M
Như vậy d ≥ E K + F I + R L = 3 E K
Mặc khác O A = a 3 3 ⇒ cos S A O ⏜ = 1 3 ⇒ sin S A O ⏜ = 2 2 3
Do đó: K E = A E sin A = a 3 2 − 2 2 3 = a 6 3
Do vậy d min = a 6

Mặt cầu (S) có tâm I(-1;2;-3), R = 5. Nhận thấy A 2 ; 2 ; 1 ∈ S . Do đó (S) là mặt cầu ngoại tiếp tứ diện vuông ABCD. Gọi G là trọng tâm tam giác BCD ta có

![]()
![]()
Vì vậy

Chọn đáp án D.
Dấu bằng xảy ra khi và chỉ khi I G ⊥ B C D ⇔ B C D : 3 x + 4 z + 20 = 0 .
Chọn đáp án D.

Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
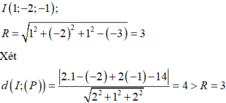
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
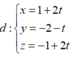
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
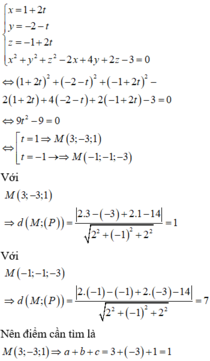

Đáp án D
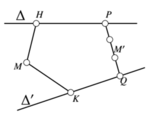
Gọi E là giao điểm của NP và CD. Gọi G là giao điểm của NP và CC’. Gọi K là giao điểm của MG và B’C’. Gọi Q là giao điểm của ME và AD. Khi đó mặt phẳng (MNP) chính là mặt phẳng (MEG). Gọi d 1 , d 2 lần lượt là khoảng cách từ C, A đến mặt phẳng (MEG). Do AC cắt (MEG) tại điểm H (như hình vẽ) nên d 1 d 2 = H C H A . Do tứ diện CMEG là tứ diện vuông tại C nên
1 d 1 2 = 1 C M 2 + 1 C E 2 + 1 C G 2
Ta có G C ' G C = C ' N C E = 1 3
Suy ra G C = 3 2 C C ' = 9 a 2
Như vậy: 1 d 1 2 = 1 a 2 + 4 9 a 2 + 4 81 a 2
Từ đó d 1 2 = 81 a 2 12 ⇒ d 1 = 9 11 . Ta có Q D M C = E D E C = 1 3 ⇒ Q D = a 3
Ta có Δ H C M đồng dạng với Δ H A Q nên:
H C H A = M C A Q = a 2 a − a 3 = 3 5 ⇒ d 1 d 2 = 3 5 ⇒ d 2 = 5 3 d 1 = 5.9 a 3.11 = 15 a 11
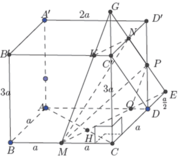

Đáp án B
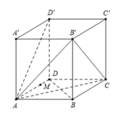
Ta có d D ; A B ' C = d B ; A B ' C mà A M A D = 3 4
Và 1 d 2 B ; A B ' C = 1 A B 2 + 1 B C 2 + 1 B B ' ⇒ d M ; A B ' C = a 2 .
Gọi E, F lần lượt là trung điểm của AD’, B’C.
Suy ra EF là đoạn vuông góc chung cuả AD’, B’C.
Do đó d A D ' ; B ' C = E F = A B = a . Vậy x y = a . a 2 = a 2 2 .