Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

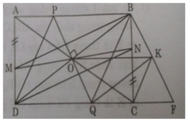
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.

a. Tứ giác ABCD là hình bình hành.
\(\Rightarrow AB=CD\)(tính chất hình bình hành)
và \(AB//CD\Rightarrow\widehat{ABD}=\widehat{BDC}\)(so le trong)
Xét \(\Delta AMB\)và \(\Delta CND\)có:
\(AB=CD\)(cmt)
\(\widehat{ABM}=\widehat{CDN}\)(cmt)
\(BM=DN\)(GT)
\(\Rightarrow\Delta AMB=\Delta CND\left(c.g.c\right)\)
b. Có AC cắt BD tại O
=> O là trung điểm của AC => OA = OC.
=> O là trung điểm của BD => OB = OD.
Có OB = OM + MD
OD = ON + ND
mà OB = OD, MB = ND
=> OM = ON => O là trung điểm của MN.
Trong tứ giác AMCN có:
OA = OC, OM = ON
=> Tứ giác AMCN có 2 đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

a: Xét tứ giác BMDN có
O là trung điểm của MN
O là trung điểm của BD
Do đó: BMDN là hình bình hành

a: Xét ΔOAN và ΔOCM có
góc AON=góc COM
OA=OC
góc OAN=góc OCM
DO đó: ΔOAN=ΔOCM
=>ON=OM
=>O là trung điểm của MN
b: Xét ΔBAC co NF//AC
nên NF/AC=BN/BA=DM/DC
Xét ΔDAC có EM//AC
nên EM/AC=DM/DC=NF/AC
=>EM=NF
mà EM=NF
nên EMFN là hình bình hành
c: Vì EMFN là hình bình hành
nen EF cắt MN tại trung điểm của mỗi đường
=>O là trung điểm của EF
=>MN,EF,AC,BD đồng quy
a, Có: hcn ABCD (gt)
=> AB // CD ( t/c )
O là trung điểm AC ( t/c ) => OA = OC.
Có: AB // CD ( cmt )
=> AN // MC
=> \(\widehat{NAO}=\widehat{MCO}\left(SLT\right)\)
Xét △ANO và △CMO có:
\(\widehat{NAO}=\widehat{MCO}\left(cmt\right)\)
OA = OC ( cmt )
\(\widehat{AON}=\widehat{COM}\left(đ^2\right)\)
=> △ANO = △CMO ( g.c.g )
=> ON = OM ( 2 cạnh tương ứng )
=> O là trung điểm MN
=> M và N đối xứng nhau qua O.
b, Có: NF // AC ( gt )
ME // AC ( gt )
=> NF // ME
=> \(\widehat{EMN}=\widehat{FNM}\left(SLT\right)\)
Có: △ANO = △CMO ( cmt )
=> \(\widehat{ENM}=\widehat{FMN}\left(2gtu\right)\)
Xét △ENM và △FMN có:
\(\widehat{ENM}=\widehat{FMN}\left(cmt\right)\)
MN chung
\(\widehat{EMN}=\widehat{FNM}\left(cmt\right)\)
=> △ENM = △FMN (g.c.g)
=> EM = FN ( 2ctu )
Mà EM // FN ( cmt )
=> ENFM là hbh ( dhnb )
Câu cuối không biết làm=)))

a) hình bình hành ABCD có:
O là giao điểm của AC và BD
=> O là trung điểm của AC và BD
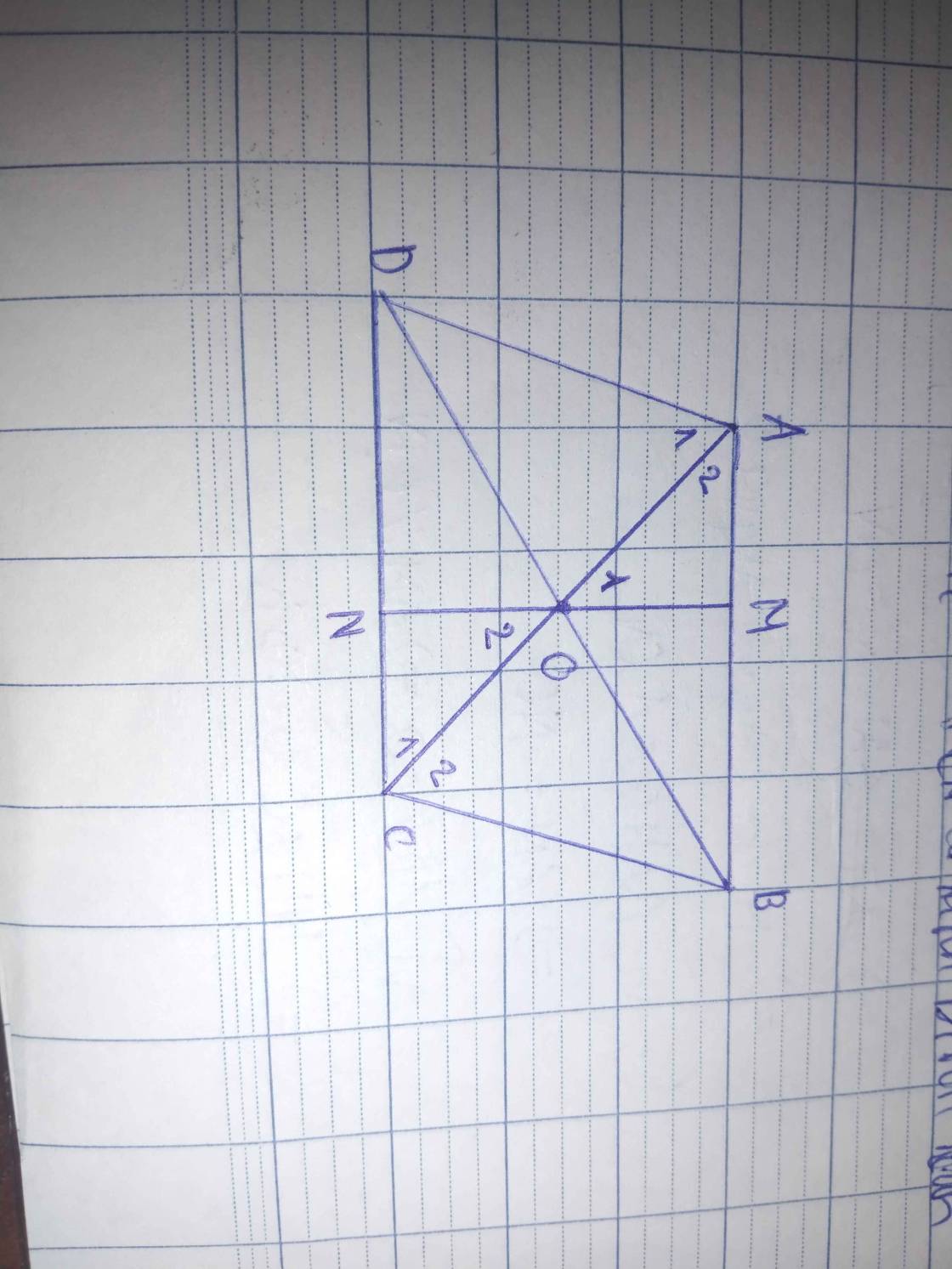
xét tam giác AOM và tam giác NOC có:
AO= CO
góc A² = góc C¹ (so le trong)
góc O¹=góc O² (đối đỉnh)
=> tam giác AOM=tam giác CON(g.c.g) => OM =ON
=> M đối xứng với N qua O
b) tam giác AOM= tam giác CON nên
=> AM= CN, AM // CN
=> tứ giác AMNC là hình bình hành