Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
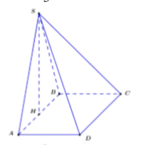
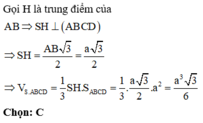

Đáp án D
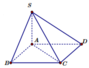
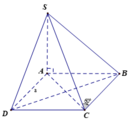
Do đáy hình vuông cạnh a nên đường chéo A C = a 2
S C ; A B C D ⏜ = A C , S C ⏜ = S C A ⏜ = 45 °
⇒ Δ S A C vuông cân tại A ⇒ S A = A C = a 2
V S . A B C D = 1 3 S A B C D . S A = 1 3 a 2 . a 2 = a 3 2 3

Đáp án D
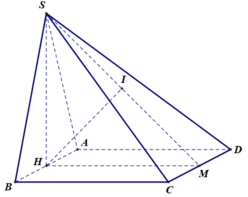
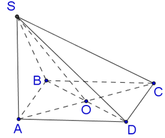
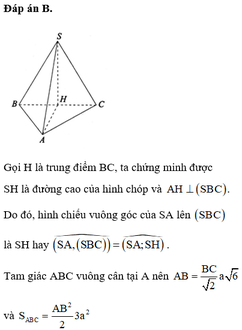
Gọi H,M lần lượt là trung điểm của AB và CD
Vì Δ S A B đều và mặt phẳng S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Ta có
C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ S H M (1)
Gọi I là hình chiếu vuông góc của H lên mặt phẳng S C D (2)
Từ (1) và (2) suy ra H I ⊥ S C D
Vì A B // C D ⇒ A B // S C D ⇒ d A , S C D = d H , S C D = H I = 3 a 7 7
Giải sử A B = x x > 0 ⇒ S H = x 3 2 H M = x .
Mặt khác: 1 H I 2 = 1 H M 2 + 1 S H 2 ⇔ 7 9 a 2 = 1 x 2 + 4 3 x 2 ⇔ x 2 = 3 a 2 ⇒ x = 3 a
Thể tích: V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 a 2 .3 a 2 = 3 a 3 2 (đvtt)



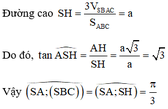
Chọn A.
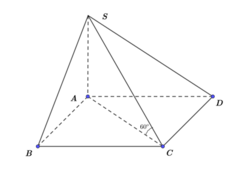
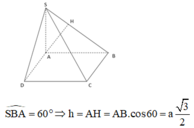
Phương pháp: Sử dụng kiến thức về góc giữa hai đường thẳng: “ Góc giữa hai đường thẳng trong không gian là góc giữa hai đường thẳng (khác) tương ứng song song (hoặc trùng) với hai đường thẳng đó. Từ đó sử dụng lượng giác và định lý
Pytago để tinh đường cao SA
Cách giải: