Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC

Câu hỏi của Phạm Thùy Dương - Toán lớp 11 - Học toán với OnlineMath
Em tham khảo bài làm tại link này nhé!
Cộng đồng học tập online | Học trực tuyến
Lần sau các bài Toán lớp 10, 11, 12 các em đăng trong trang Cộng đồng học tập online | Học trực tuyến nhé! olm hầu như để giải đáp thắc mắc của HỌc sinh tiểu học và trung học em nhé :). Chúc em học tập tốt :)<3

Chọn D
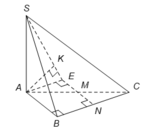
Xác định được
![]()
![]()
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
![]()
![]()

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

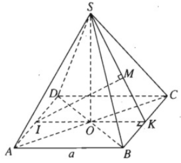
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 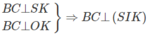
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 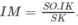
Ta lại có:
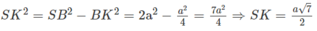
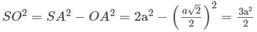
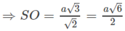
Do đó:
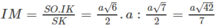
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 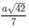
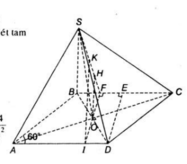

Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.