Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
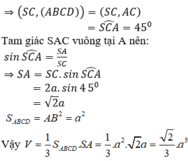

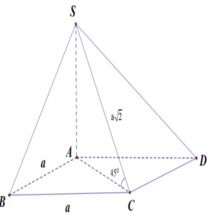
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
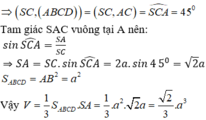

Lời giải:
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)

mình nghĩ câu hỏi của bạn chắc là nhầm thì phải.đáp án diện tích phải là:8π\(a^2\)
có phải bạn muốn tìm bán kính mặt cầu ngoại tiếp ko?nếu tìm bán kính ta làm như sau:SA=tan(60).AC=\(\sqrt{6}\)a
gọi O là tâm đáy suy ra AO=\(\frac{a\sqrt{2}}{2}\).từ O kẻ đt d vuông góc vs đáy .gọi Mlà trung điểm SA.trong mp(SAO) từ Mkẻ đt vuông góc SA cắt d tại I. I là tâm mặt cầu
R=IA=\(\sqrt{AI^2+AO^2}=a\sqrt{2}\)

Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)
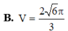
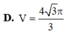
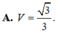
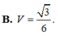
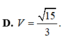

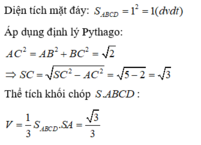

Đáp án A