Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD.\)
\(ABCD\) là hình vuông \(\Rightarrow CD\perp AD.\)
\(\Rightarrow CD\perp\left(SAD\right).\)
\(\Rightarrow A\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)
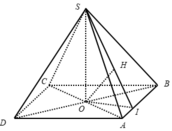
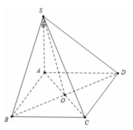
- Gọi O là giao điểm của AC và BD.
- Kẻ: OI ⊥ AB, OH ⊥ SI.
+) Ta có:
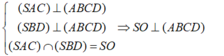
+) Ta lại có:
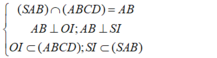
- Do đó, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng góc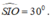 
+) Khi đó: CD // AB nên CD // ( SAB).
Suy ra:
- Ta có:
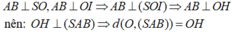
+) Tam giác ABC có BC = BA và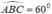 
nên tam giác ABC đêù
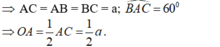
- Trong tam giác OIA có:
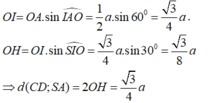
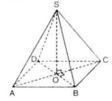
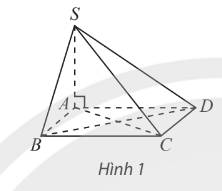
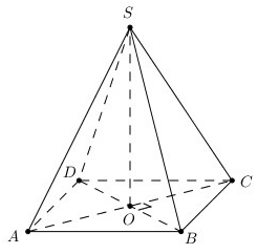
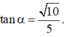
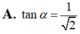
Chọn C, bởi vì AC ko thể vuông góc với SB và SD được mà chỉ có thể vuông góc với BD thôi