


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





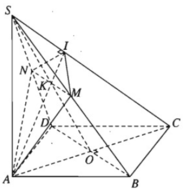
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 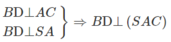
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

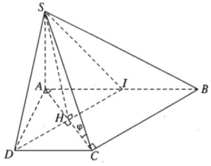
a) Ta có:
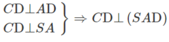
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
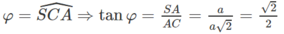
c) 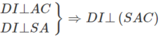
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 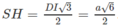 .
.
Tam giác SDI có diện tích:
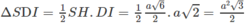

Bạn vẽ hình giúp mình nha ^^
Xét (ABCD), kẻ \(MH\perp AB\left(H\in AB\right)\)
Xét (SAB), kẻ HF//SB(\(F\in SA\))
Có: \(\left\{{}\begin{matrix}MH\perp AB\\MH\perp SA\end{matrix}\right.\)\(\Rightarrow MH\perp\left(SAB\right)\)\(\Rightarrow MH\perp HF\)
Ta có: \(\alpha=\left(\stackrel\frown{SB,AM}\right)=\left(\stackrel\frown{HF,MH}\right)=arccos\left(\dfrac{HA}{HF}\right)\)
Xét \(\Delta AHF\) vuông tại A có: \(HF^2=HA^2+AF^2=a^2+\left(\dfrac{a}{2}\right)^2=\dfrac{5}{4}a^2\Rightarrow HF=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow\alpha=arccos\left(\dfrac{HA}{HF}\right)=arccos\left(\dfrac{2a}{a\sqrt{5}}\right)\approx26,57^o\) \(\Rightarrow cos\alpha=\dfrac{HA}{HF}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
là \(cos^{-1}\) trong máy tính á, đại loại kiểu ngược lại của cos... sin/cos/tan/sin sẽ đi với góc, còn arc + sin/cos/tan/cot là các cạnh ứng với công thức sin/cos/tan/cot

CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SC;(SAD))=(SC;SD)=góc DSC
SD=căn SA^2+AD^2=a*căn 7
DC=a
SC=căn SA^2+AC^2=3a
\(cosDSC=\dfrac{SD^2+SC^2-DC^2}{2\cdot SD\cdot SC}=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{5\sqrt{7}}{14}\)
=>góc DSC=19 độ

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)