Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
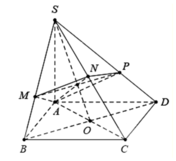
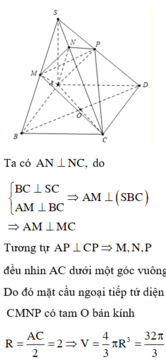
Nối S O ∩ A N = E , qua E kẻ đường thẳng song song với BD. Cắt SB,SD lần lượt tại M , P ⇒ m p P ≡ A M N P .
Ta có S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ A B C D ⇒ B C ⊥ S A B .
Mà SC ⊥ A M N P ⇒ S C ⊥ A M suy ra A M ⊥ S B C .
Do đó A M ⊥ M C mà O là trung điểm của A C ⇒ O A = O M = O C .
Tương tự, ta chứng minh được O là tâm mặt cầu ngoại tiếp khối
đa diện A B C D . M N P ⇒ R = A C 2 = 4 a 3 2 = 2 a 3 .
Vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 3 3 = 32 3 π a 3 .

Đáp án B.
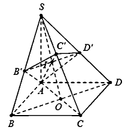
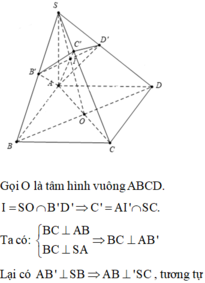
Gọi O là tâm của hình vuông ABCD, nối S O ∩ B ' D ' = I .
Và nối AI cát SC tại C’ suy ra mp (AB’D’) cắt SC tại C’.
Tam giác SAC vuông tại A, có S C 2 = S A 2 + A C 2 = 6 a 2 ⇒ S C = a 6 .
Ta có B C ⊥ S A B ⇒ B C ⊥ A B ' và S B ⊥ A B ' ⇒ A B ' ⊥ S C .
Tương tự A D ' ⊥ S C suy ra S C ⊥ ( A B ' D ' ) ≡ ( A B ' C ' D ' ) ⇒ S C ⊥ A C ' .
Mà S C ' . S C = S A 2 ⇒ S C ' S C = S A 2 S C 2 = 2 3 và S B ' S B = S A 2 S B 2 = 4 5 .
Do đó V S . A B ' C ' = 8 15 V S . A B C = 8 30 V S . A B C D mà V S . A B C D = 1 3 . S A . S A B C D = 2 a 3 3 .
Vậy thể tích cần tính là V S . A B ' C ' D ' = 2 . V S . A B ' C ' = 16 a 3 45

Đáp án D.
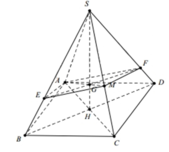
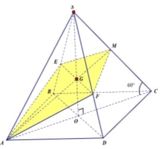
Gọi H là tâm của hình vuông A B C D ; S B H ^ = 60 0 ; H B = a 2 2
Khi đó là trọng tâm tam giác SAC.
Qua G dựng đường thẳng song song với BD cắt SB;SD lần lượt là E và F.
Do tính chất đối xứng ta có:
V S . A E M F V S . A B C D = V S . A E M V S . A B C = S E S B . S M S C = 2 3 . 1 2 = 1 3 .
Mặt khác V A . A B C D = 1 3 S H . S A B C D = 1 3 H B tan 60 0 . a 2 = a 3 6 6 .
Do đó V S . A E M F = 1 3 . a 3 6 6 = a 3 6 18 .


Do
![]()
và S A ' = 1 3 S A nên

Chọn: C
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng cho hình chóp tam giác.

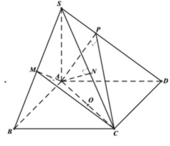

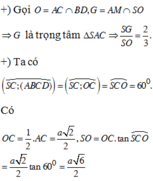

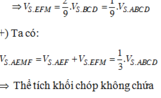
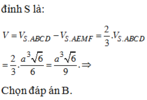

Chọn D.
Phương pháp:
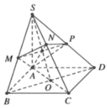
+ Chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện CMNP (với O là tâm của hình vuông ABCD)