Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hôm nay đi cắt lại cái kính, uay đi uay lại mất luôn buổi sáng :(

Bài này để sáng mai thử nghĩ coi sao nhó :) Giờ đi học hóa đã, rảnh inbox tui tán chuyện phiếm xí, dạo này ông anh đi làm đồ án chán chả có ai ngồi nói chuyện cùng :(

a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)

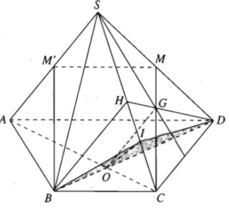
a) Gọi H là trung điểm của SC
Ta có:
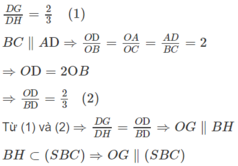
b) Gọi M’ là trung điểm của SA ⇒ MM′ // AD và MM′ = AD/2.
Mặt khác vì BC // AD và BC = AD/2 nên BC // MM′ và BC = MM′.
Do đó tứ giác BCMM’ là hình bình hành ⇒ CM // BM′ mà BM′ ⊂ (SAB)
⇒ CM // (SAB)
c) Ta có: 
Mặt khác vì 
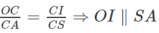
OI ⊂ (BID) ⇒ SA // (BID)

Vẫn dùng kĩ thuật cũ:
\(\overrightarrow{AD}-2\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}-2\overrightarrow{BS}-2\overrightarrow{SC}=0\)
\(\Leftrightarrow\overrightarrow{SA}=2\overrightarrow{SB}-2\overrightarrow{SC}+\overrightarrow{SD}\) (1)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SN}\)
Giả thiết suy ra \(\overrightarrow{SD}=3\overrightarrow{SM}\)
Thế vào (1): \(\overrightarrow{SA}=2\overrightarrow{SB}-2x.\overrightarrow{SN}+3\overrightarrow{SM}\)
Do A, B, N, M đồng phẳng
\(\Rightarrow2-2x+3=1\)
\(\Rightarrow x=2\Rightarrow SC=2SN\Rightarrow SN=\dfrac{1}{2}SC\)
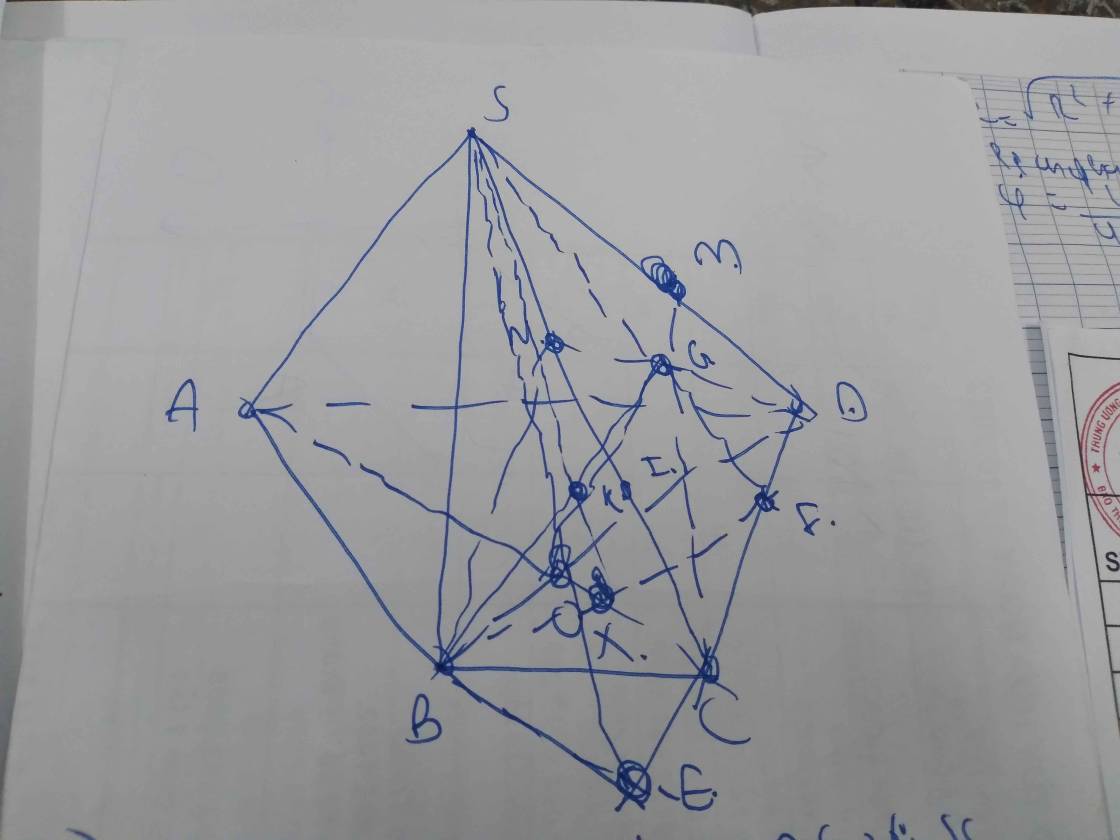
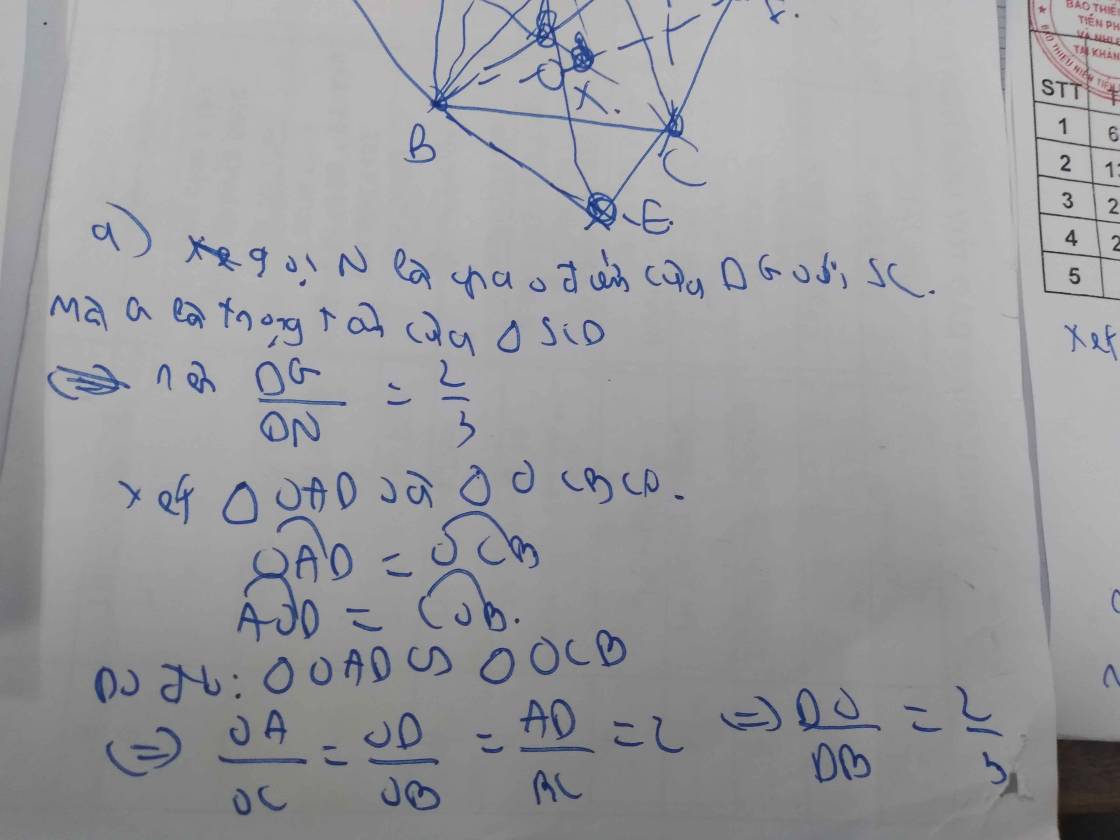







Bài làm:
a) Do BC//AD và AD\(\subset\) (SAD)
=> BC// (SAD)
b) có \(\dfrac{DE}{AE}=\dfrac{DN}{NS}=2\)
=> NE//SA
do BC//AD => \(\dfrac{BC}{AD}=\dfrac{OB}{OD}=\dfrac{1}{2}\) => \(\dfrac{DE}{AE}=\dfrac{OD}{OB}=2\) => OE//AB
Do NE//SA và OE//AB mà OE,NE \(\subset\)(ONE); SA,SB\(\subset\) (SAB)
=> (ONE) //(SAB)