Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

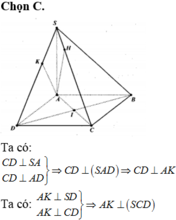
Chọn C.
Phương pháp:
Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu.
Cách giải
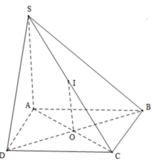
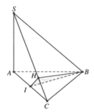
Gọi I là trung điểm của đoạn thẳng SC.
O là tâm của hình chữ nhật ABCD.
Ta chứng minh I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD:
Do OI là đường trung bình của tam giác SAC => OI // SA


Đáp án D
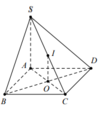
Vì O,I lần lượt là trung điểm của AC,SC. Suy ra OI//SA mà S A ⊥ A B C D ⇒ O I ⊥ A B C D .
S A ⊥ A B C D ⇒ S A ⊥ B D mà B D ⊥ A C ⇒ B D ⊥ S A C .
Ta có S A ⊥ C D A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D ⇒ ∆ S C D vuông tại D.
Suy ra ID = IC tương tự ta được I B = I C ⇒ I A = I B = I C = I D .
BC không vuông góc với mặt phẳng (SCD) vì S C B ^ < 90 °
Vậy có hai khẳng định đúng là 1 và 3.

Đáp án A
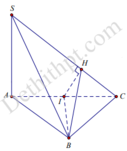
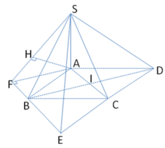
Vì Δ A B C cân tại B nên I là trung điểm của AC nên B I ⊥ A C .
Ta có:
S A ⊥ B I , B I ⊥ A C ⇒ B I ⊥ S A C ⇒ B I ⊥ S C
mà
S C ⊥ I H ⇒ S C ⊥ B I H ⇒ S B C ⊥ B I H .
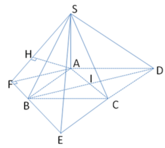
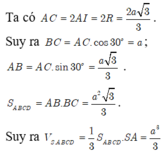
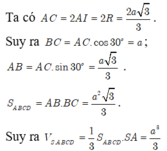

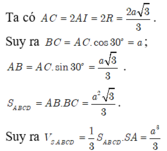


Đáp án A