Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

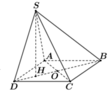
Xác định được ![]()
Tính được ![]()
![]()
Suy ra tam giác SBD vuông tại S. Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên ![]()
Chọn B.

Đáp án C
Gọi O là trung điểm của SD. Ta có: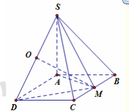
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .

Đáp án A
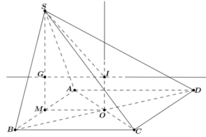
Gọi N là trung điểm của MD, khi đó N là tâm đường tròn ngoại tiếp tam giác vuông ADM.
Dựng đường thẳng Δ đi qua N và song song với SA⇒Δ là trục đường tròn ngoại tiếp tam giác ADM.
Dựng mặt phẳng trung trực (P) của SA, P ∩ Δ = I , khi đó I là tâm của mặt cầu ngoại tiếp hình chóp SADM, bán kính R = IA .
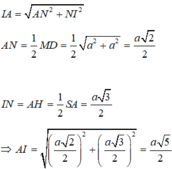
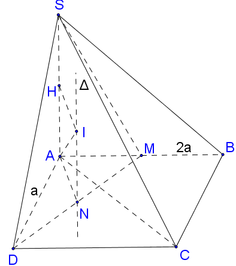

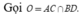
Vì ABCD là hình vuông nên OA = OB = OC (1)
Dễ dàng chứng minh được A H ⊥ H C nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC
Từ (1) và (2) suy ra ![]()
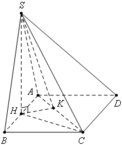


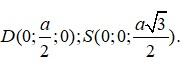
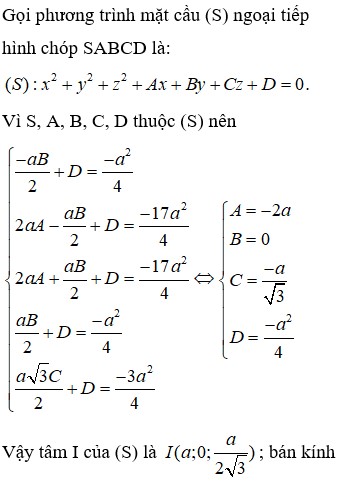




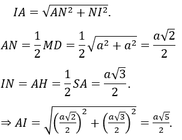
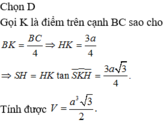
Đáp án B
Tam giác HCD vuông tại C ⇒ H D = H C 2 + C D 2 = a 6 2
Tam giác BCD vuông tại C ⇒ sin C B D ⏜ = C D B D = 1 3
Suy ra bán kính đường tròn ngoại tiếp Δ H B D là
R Δ H B D = H D 2. sin H B D ⏜ = a 6 2 : 2 3 = 3 a 2 4
Bán kính mặt cầu cần tính là R = R Δ H B D 2 + S H 2 4 = a 5 2