Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

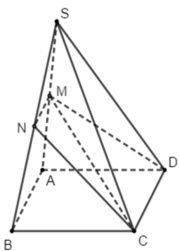
Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.
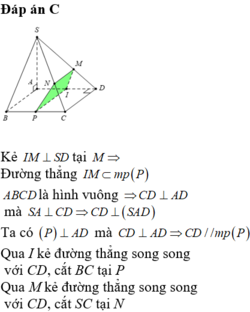
Đáp án C

Đáp án D
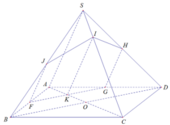
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD
d cắt AD tại G
d cắt AC tại K ⇒ F G ∩ A C = K
Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA
x cắt SD tại H
Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA
y cắt SB tại J
Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA
z cắt AC tại I
⇒ FGHIK là thiết diện cần tìm
⇒ thiết diện là ngũ giác

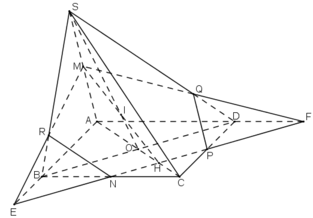
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
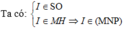
Vậy I = SO ∩ (MNP).

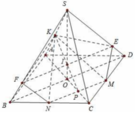
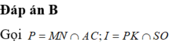
Do MN//BD nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD,SB lần lượt tại E và F khi đó thiết diện là ngũ giác KEMNF

trong mặt phẳng (SAC) : SO ∩ CI = K là trọng tâm tam giác SAC
Trong mặt phẳng (SBD): BK ∩ SD = J là trung điểm SD ⇒ IJ // AD ⇒ IJ // BC.
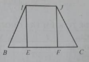
∆SAB = ∆SCD (c.c.c) ⇒ trung tuyến BI = CJ ⇒ thiết diện CBIJ là hình thang cân.
Đáp án D
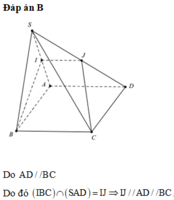
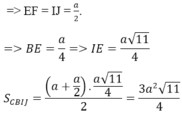
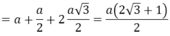
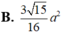
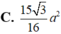


Ta có BC//AD (cạnh đối hình bình hành) (1)
Trong mp (SAD) từ I dựng đường thẳng // với AD cắt SD tại K
=>IK//AD (2)
Từ (1) và (2) => IK//BC
\(I\in\left(IBC\right)\Rightarrow IK\in\left(IBC\right)\)
=> BCKI là thiết diện của (IBC) với S.ABCD và BCKI là hình thang
Gọi J là trung điểm của SA. Ta thấy IJ//AD//BC nên J, I, B, C đồng phẳng \(\Rightarrow J\in\left(IBC\right)\).
Ta có \(I=\left(IBC\right)\cap SA,B=\left(IBC\right)\cap SB,C=\left(IBC\right)\cap SC,\) \(J=\left(IBC\right)\cap SD\), suy ra tứ giác BCJI là thiết diện của hình chóp S.ABCD cắt bởi mặt (IBC)
Mà BC//JI (cmt) nên BCJI là hình thang \(\Rightarrowđpcm\)