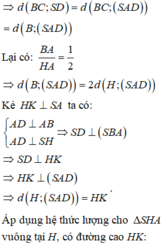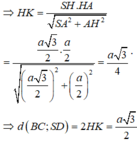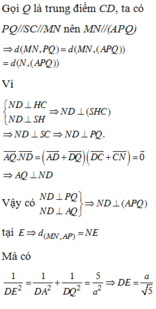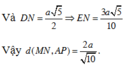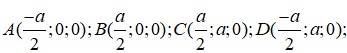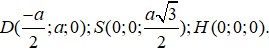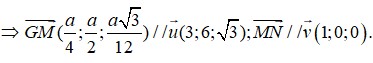Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
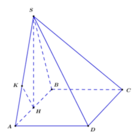
Gọi h là trung điểm của A B ⇒ S H ⊥ A B C D
Kẻ H K ⊥ S A K ∈ S A ⇒ H K ⊥ S A D ⇒ d H ; S A D = H K
Vì A D / / B C ⇒ B C / / m p S A D ⇒ d S A ; B C = d B C ; S A D
= d B ; S A D = 2 × d H ; S A D = 2 H K
Tam giác SAH vuông tại H, có H K = S H . H A S H 2 + H A 2 = a 3 4
Vậy d S A ; B C = 2 H K = 2. a 3 4 = a 3 2

Chọn đáp án C
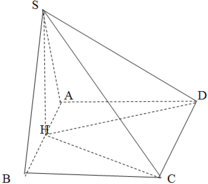
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên S O ⊥ A B C D
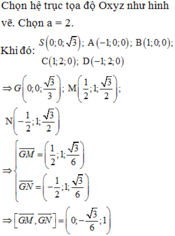
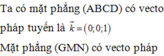

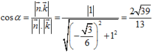

Đáp án C.
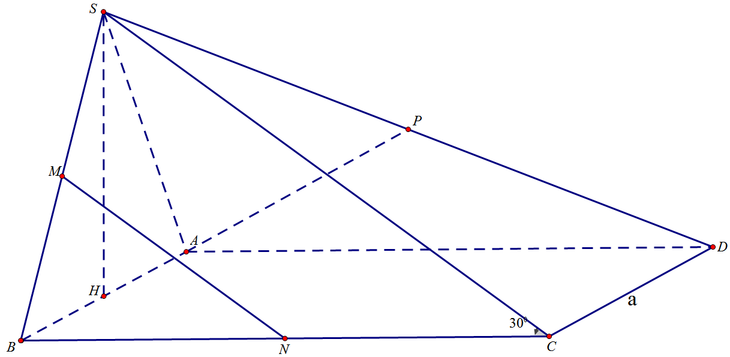
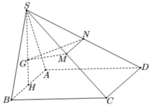
Trong không gian Oxyz:
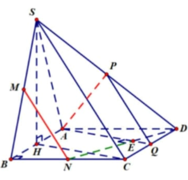
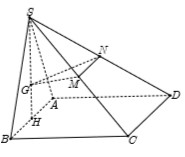
Chọn A ≡ O 0 ; 0 ; 0 ; B a ; 0 ; 0 ; D 0 ; a ; 0 ; C a ; a ; 0
⇒ H a 2 ; 0 ; 0 ; S a 2 ; 0 ; a 3 2 ; M 3 a 4 ; 0 ; a 3 4 ; N a ; a 2 ; 0 ; P a 4 ; a 2 ; a 3 4
Ta có:
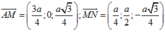
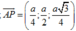

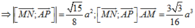
⇒ d M N ; A P = M N → ; A P → . A M → M N → ; A P → = 3 5 10 a

Đáp án C

Gọi H, M lần lượt là trung điểm của AD, BC.
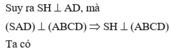
AD // (SBC) Þ d(AD, SC) = d(AD,(SBC)) = d(H,(SBC))
Trong tam giác SHM kẻ HK ^ SM tại K