Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ O kẻ OH vuông góc với SB, H ∈ SB ⇒ d(O; SB) = OH.
+ Ta có AB = BC = 2a; A B C ^ = 60 ° ⇒ Tam giác ABC đều có BO ⊥ AC
⇒ BO = 2a. 3 2 = a 3
AO = A C 2 = 2 a 2 = a
SO = S A 2 + A O 2 = 4 a 2 + a 2 = a 5
+ Ta có B D ⊥ A C ( h t h o i A B C D ) B D ⊥ S A S A ⊥ A B C D ⇒ B D ⊥ S A C ⇒ B D ⊥ S O
Tam giác SOB vuông tại O
Do đó: 1 O H 2 = 1 S O 2 + 1 O B 2 = 1 5 a 2 + 1 3 a 2 ⇒ OH = a. 30 4
Vậy d(O; SB) = OH = a 30 4 .
Đáp án C

lại là chuyên mục toán hình :)) ( P/s hình t lấy từ gg xuống vì trên này khó vẽ... )
Ta có: \(\cos\left(\widehat{SB,AC}\right)=\left|\cos\left(\overrightarrow{SB},\overrightarrow{AC}\right)\right|=\dfrac{\left|\overrightarrow{SB}.\overrightarrow{AC}\right|}{SB.AC}\)
Mà: \(\overrightarrow{SB}.\overrightarrow{AC}=\left(\overrightarrow{SA}+\overrightarrow{AB}\right).\overrightarrow{AC}=\overrightarrow{SA}.\overrightarrow{AC}+\overrightarrow{AB}.\overrightarrow{AC}\)
\(=SA.AC.\cos\left(\overrightarrow{SA},\overrightarrow{AC}\right)+AB.AC.\cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)\)
thay số các kiểu ta đc \(\overrightarrow{SB}.\overrightarrow{AC}=a^2\) (1)
Hoàn toàn dễ dàng tính được \(SB=\sqrt{SA^2+AB^2}=2a\) ( tam giác SAB vuông tại A )
\(\Rightarrow SB.AC=2\sqrt{2}a^2\) (2)
Từ (1),(2) \(\Rightarrow\cos\left(\widehat{SB,AC}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Rightarrow\left(\widehat{SB,AC}\right)\simeq69^0\)
có 17' nữa t định ghi mà sợ ông kêu số xấu sai kết quả :)))


bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!

Đáp án A
Trong mặt phẳng dựng đường thẳng đi qua A và vuông góc vưới SB tại K
Ta chứng minh được
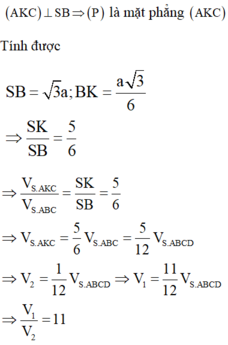

a.
Do AD song song BC nên góc giữa SD và BC là góc giữa SD và AD, cùng là góc \(\widehat{SDA}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{1}{8}\)
\(\Rightarrow\widehat{SDA}=82^049'\)
b.
Do chóp có các cạnh bên bằng nhau và đáy là hình vuông nên chóp là chóp đều
Gọi O là tâm đáy \(\Rightarrow AC\perp BD\) tại O và \(SO\perp\left(ABCD\right)\)
\(\Rightarrow\Delta OCD\) là hình chiếu vuông góc của tam giác SCD lên (ABCD)
\(OC=OD=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2AB^2}=a\sqrt{2}\)
\(\Rightarrow S_{OCD}=\dfrac{1}{2}OC.OD=a^2\)

Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah