Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

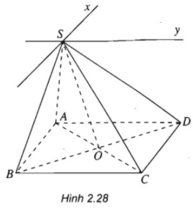
a)
Ta có:
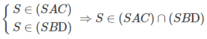
Giả sử:
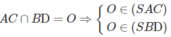
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
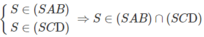
Ta lại có
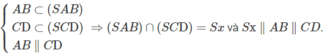
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.

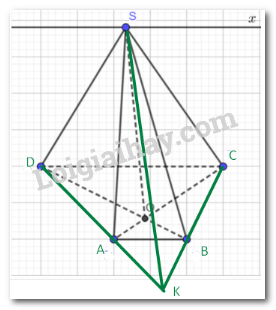
a, Gọi \(I=AC\cap BD\)
Mà \(AC\in\left(SAC\right);BD\in\left(SBD\right)\)
\(\Rightarrow I=\left(SAC\right)\cap\left(SBD\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SI\) là giao tuyến cần tìm.
b, Gọi \(K=AC\cap BM\)
Mà \(AC\in\left(SAC\right);BM\in\left(SBM\right)\)
\(\Rightarrow K=\left(SAC\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBM\right)\Rightarrow SK\) là giao tuyến cần tìm.
c, Gọi \(N=AD\cap BM\)
Mà \(AD\in\left(SAD\right);BM\in\left(SBM\right)\)
\(\Rightarrow N=\left(SAD\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAD\right)\cap\left(SBM\right)\Rightarrow SN\) là giao tuyến cần tìm.
d, Gọi \(T=AM\cap BC\)
Mà \(AM\in\left(SAM\right);BC\in\left(BMC\right)\)
\(\Rightarrow T=\left(SAM\right)\cap\left(SBC\right)\)
Lại có \(S=\left(SAM\right)\cap\left(SBC\right)\Rightarrow ST\) là giao tuyến cần tìm.

a: Gọi O là giao của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Xét (SBC) và (SAD) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SBC) giao (SAD)=xy, xy đi qua S và xy//AD//BC

a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).

Gọi giao điểm của AC và BD là K
\(K\in AC\subset\left(SAC\right)\)
\(K\in BD\subset\left(SBD\right)\)
Do đó: \(K\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SK\)
Gọi giao điểm của AB và CD là H
\(H\in AB\subset\left(SAB\right)\)
\(H\in CD\subset\left(SCD\right)\)
Do đó: \(H\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SH\)
Gọi M là giao điểm của AD và BC
\(M\in AD\subset\left(SAD\right)\)
\(M\in BC\subset\left(SBC\right)\)
Do đó: \(M\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SM\)
\(P\in SD\subset\left(SCD\right)\)
\(P\in\left(PAB\right)\)
Do đó: \(P\in\left(SCD\right)\cap\left(PAB\right)\)(1)
\(H\in AB\subset\left(PAB\right);H\in CD\subset\left(SCD\right)\)
Do đó: \(H\in\left(PAB\right)\cap\left(SCD\right)\)(2)
Từ (1) và (2) suy ra \(\left(SCD\right)\cap\left(APB\right)=HP\)

d: \(CD\subset\left(HKCD\right)\)
\(CD\subset\left(ABCD\right)\)
Do đó: \(\left(HKCD\right)\cap\left(ABCD\right)=CD\)
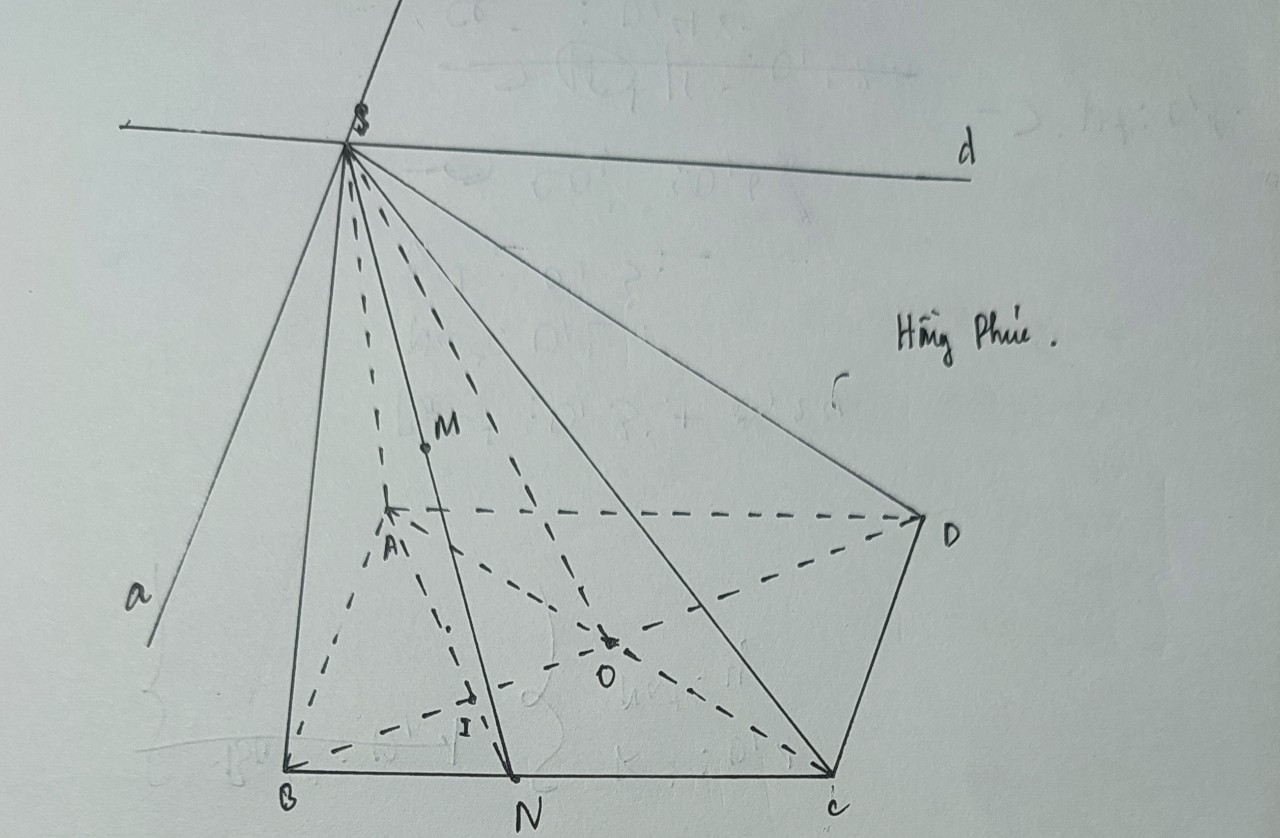
a: \(O\in BD\subset\left(SBD\right)\)
\(O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SO\)
b: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c; AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC


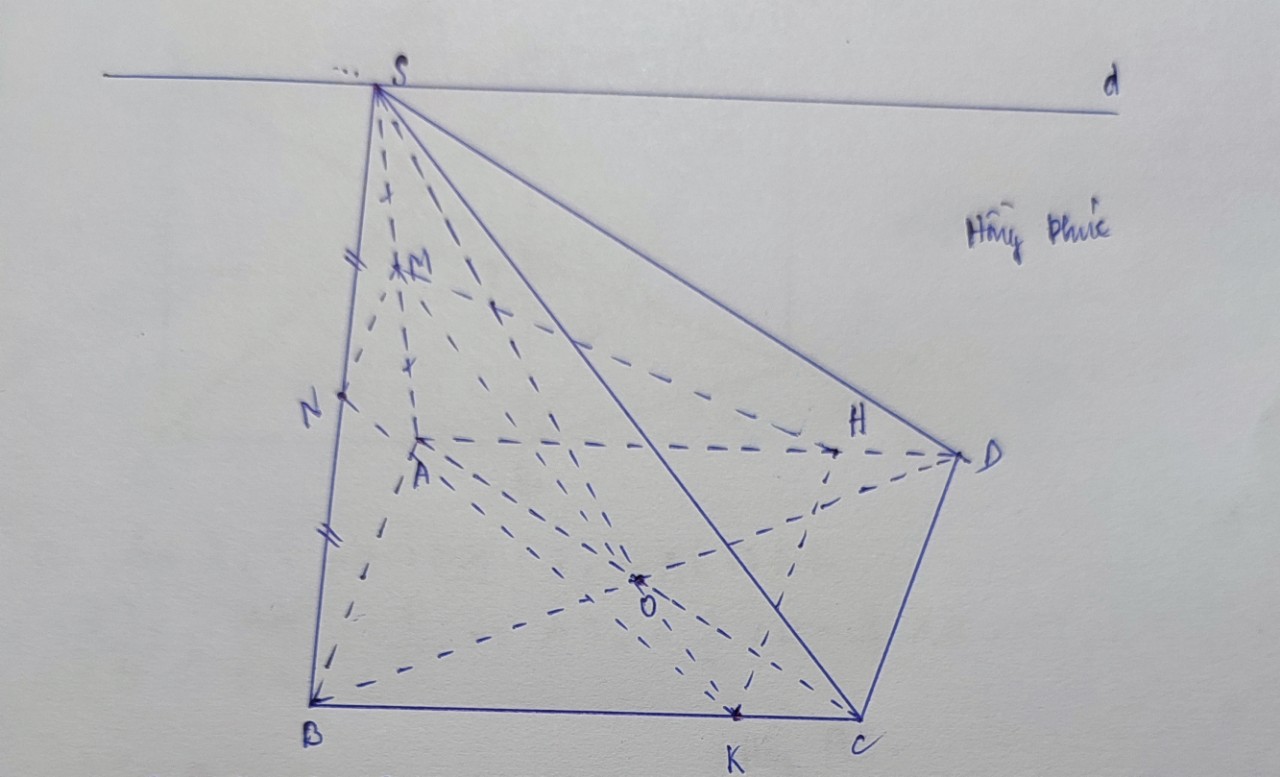
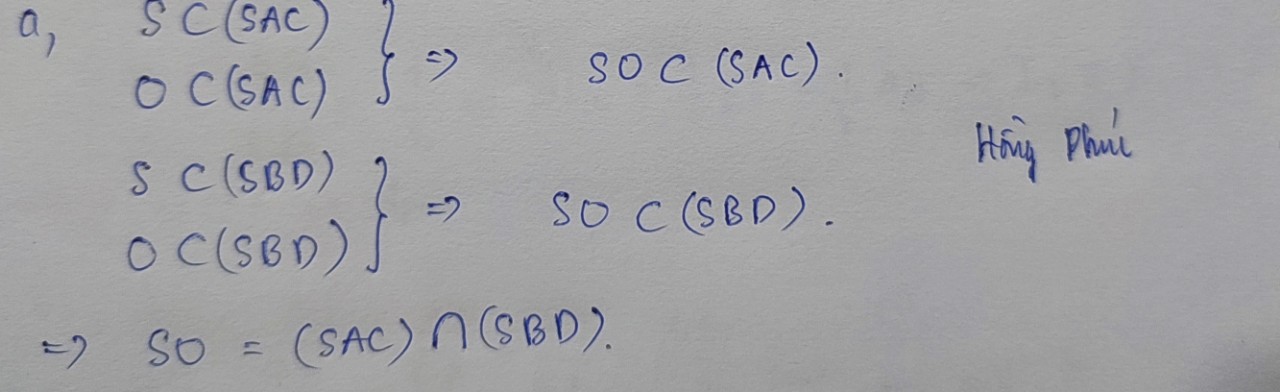
a/ \(\left\{{}\begin{matrix}S\in SB\subset\left(SBC\right)\\S\in SC\subset\left(SCD\right)\end{matrix}\right.\Rightarrow S=\left(SBC\right)\cap\left(SCD\right)\)
\(\left\{{}\begin{matrix}C\in SC\subset\left(SBC\right)\\C\in SC\subset\left(SCD\right)\end{matrix}\right.\Rightarrow C=\left(SBC\right)\cap\left(SCD\right)\)
\(\Rightarrow\left(SBC\right)\cap\left(SCD\right)=SC\)
b/ Gọi O là giao điểm của AC và BD
\(\Rightarrow\left\{{}\begin{matrix}O=\left(SAC\right)\cap\left(SBD\right)\\S=\left(SAC\right)\cap\left(SBD\right)\end{matrix}\right.\Rightarrow\left(SBD\right)\cap\left(SAC\right)=SO\)
c/ \(\left\{{}\begin{matrix}S=\left(SAD\right)\cap\left(SBC\right)\\Sx//AD//BC\end{matrix}\right.\Rightarrow\left(SAD\right)\cap\left(SBC\right)=Sx\)