Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

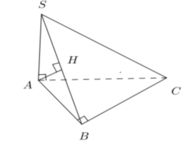
- Kẻ AH ⊥ SB (1)
- Ta có:
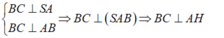
- Suy ra:
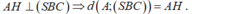
- Trong tam giác vuông ΔSAB ta có:
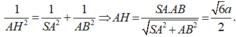

Đáp án B
HDG:
![]()
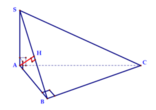
Dễ dàng chứng minh ∆ S B C vuông tại B
![]()
![]()
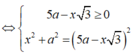
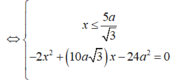
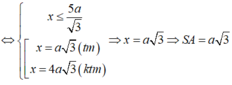
Ta có (SAB) ⊥ (SBC) theo giao tuyến SB. Kẻ
![]()
![]()

Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)

Chọn đáp án D
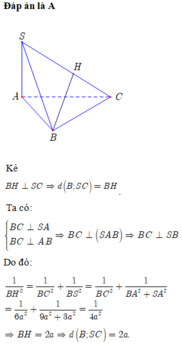
+ Gọi H là trung điểm SB. Do tam giác SAB vuông tại A, SBC vuông tại C suy ta HA = HB = HS = HC
Suy ra H là tâm mặt cầu.
+ Gọi I là hình chiếu của H lên (ABC). Do HA = HB = HC , suy ra IA = IB = IC
Suy ra I là trung điểm AC. Gọi P là trung điểm BC, do tam giác ABC vuông cân, suy ra
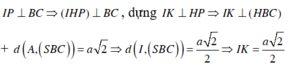
Áp dụng hệ thức
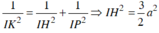
\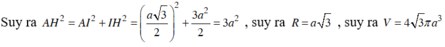

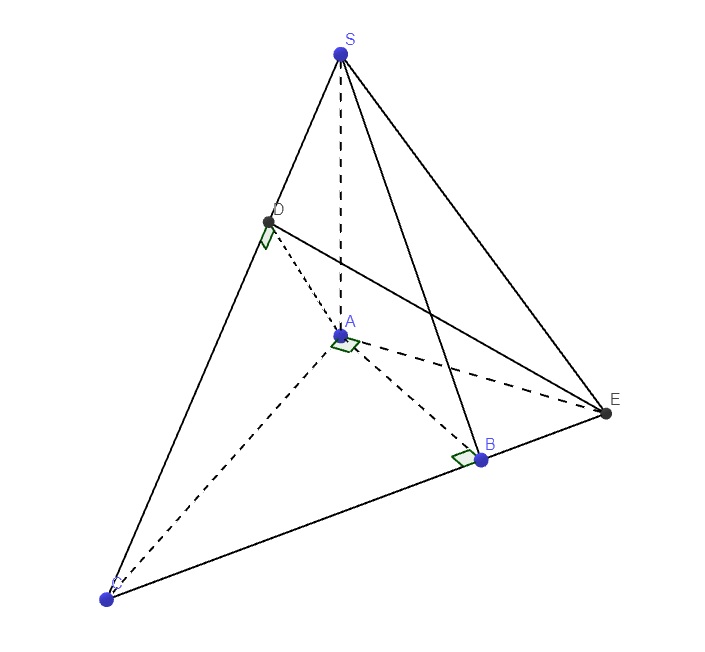
Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ

Chọn D.
- Kẻ AH ⊥ SB.
- Ta có:
- Trong tam giác vuông SAB ta có: