Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ

a) Ta có:
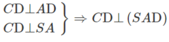
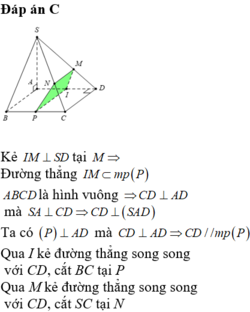
⇒ (SCD) ⊥ (SAD)
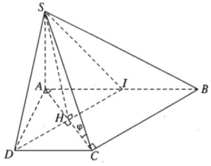
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
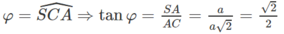
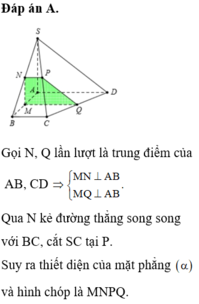
c) 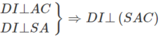
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 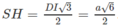 .
.
Tam giác SDI có diện tích:
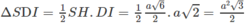

a.
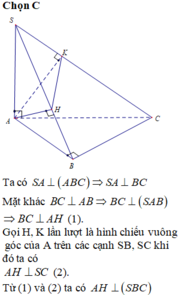
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
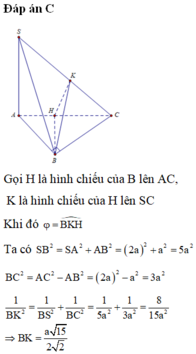





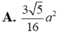
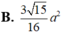
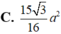


c.
Từ M kẻ \(MH\perp SC\) (H thuộc SC)
\(\Rightarrow H\in\left(\alpha\right)\Rightarrow\) thiết diện là tam giác BMH
Do \(\left\{{}\begin{matrix}BM\perp\left(SAC\right)\\MH\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow BM\perp MH\Rightarrow\Delta BMH\) vuông tại M
Trong tam giác vuông ABC: \(BM=\dfrac{1}{2}AC=a\) (trung tuyến ứng với cạnh huyền)
Hai tam giác vuông CHM và CAS đồng dạng (chung góc C)
\(\Rightarrow\dfrac{MH}{SA}=\dfrac{CM}{SC}\Rightarrow MH=\dfrac{SA.CM}{SC}=\dfrac{SA.\dfrac{AC}{2}}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\Rightarrow S_{BMH}=\dfrac{1}{2}BM.MH=\dfrac{a^2\sqrt{5}}{10}\)