Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

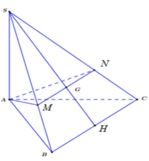
Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
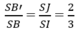
Do đó dễ thấy
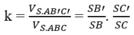

Đáp án C
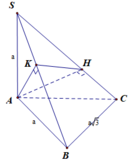
Ta có
![]()
![]()
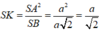
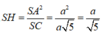
V S . A H K V S . A B C = S K . S H S B . S C = 1 10
⇒ V S . A H K = 1 10 V S . A B C = 1 60 3 a 3

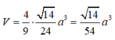

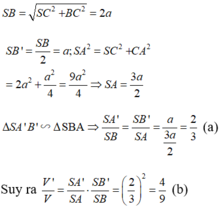
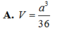
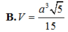

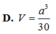
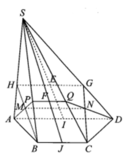
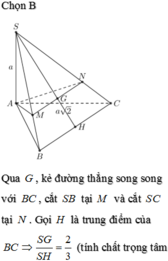
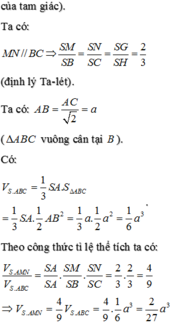
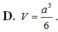



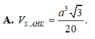
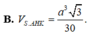
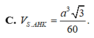

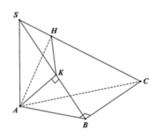

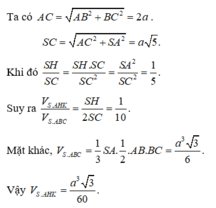
Chọn B.
Dễ thấy AB ⊥ BC. Suy ra SB ⊥ BC, ∆ SMN đồng dạng với ∆ SCB, do đó