Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
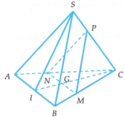
c os S M ; B C = c os S M → ; B C → = S M → . B C → S M . B C , ta có S M = a 2 2 ; B C = a 2 ;
S
M
→
.
B
C
→
=
1
2
S
B
→
+
S
A
→
S
C
→
−
S
B
→
=
−
1
2
S
B
2
=
−
1
2
a
2
;
c
os
S
M
;
B
C
^
=
1
2
⇒
S
M
;
B
C
^
=
60
∘

Đáp án C
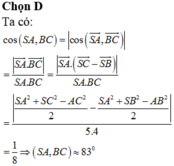
Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có: S O ⊥ A B C
Do A E = B C S O = B C ⇒ B C ⊥ S A E . Dựng E K ⊥ A suy ra EK là đoạn vuông góc cung của SA và BC. Tương tự dựng FI; RL là các đoạn vuông góc chung của 2 cạnh đối diện.
Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M
Như vậy d ≥ E K + F I + R L = 3 E K
Mặc khác O A = a 3 3 ⇒ cos S A O ⏜ = 1 3 ⇒ sin S A O ⏜ = 2 2 3
Do đó: K E = A E sin A = a 3 2 − 2 2 3 = a 6 3
Do vậy d min = a 6

Đáp án C
Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có S O ⊥ A B C .
Do A E ⊥ B C S O ⊥ B C ⇒ B C ⊥ ( S A E ) .
Dựng E K ⊥ S A suy ra EK là đoạn vuông góc chung cua SA và BC.
Tương tự dựng FI; RL là các đoạn vuông góc chung cùa 2 cạnh đoi diện. Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M. Như vậy d ≥ K + F I + R L = 3 E K
Mặt khác K E = a 3 2 ⇒ cos S A O ^ = 1 3 ⇒ s i n S A O ^ = 2 2 3
Do đó K E = A E . sin A = a 3 2 . a 2 3 = a 6 3
Do vậy d m i n = a 6 .

Đáp án C
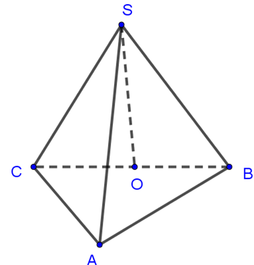
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
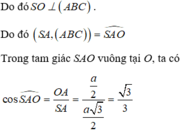

Chọn đáp án D
Ta có
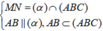
![]()
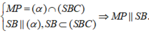
![]()
Khi đó ![]()
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
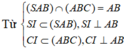
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0