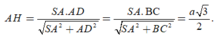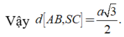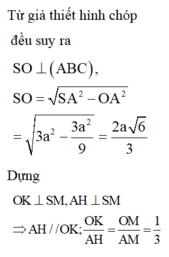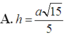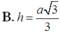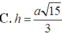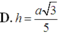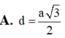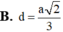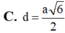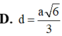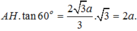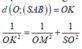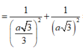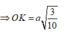Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

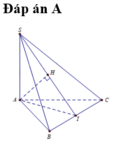
Chọn A
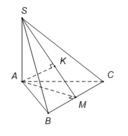
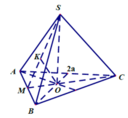
Gọi M là trung điểm BC
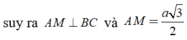
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
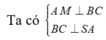
![]()
![]()
![]()
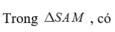
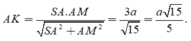
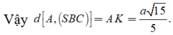

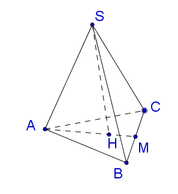
Ta tính được \(AG=a\dfrac{\sqrt{3}}{3}\)
Từ gt ta có:
\(\widehat{\left(SA,\left(ABC\right)\right)}=\widehat{\left(SA,AG\right)}=\widehat{SAG}=60^0\)(Vì S.ABC là chóp tam giác đều nên \(SG\perp\left(ABC\right)\))
Khi đó SG=AG.tan60=a
Gọi M là trung điểm BC \(\Rightarrow GM=a\dfrac{\sqrt{3}}{6}\)
Đặt d(G,(SBC))=x
Áp dụng mô hình "điểm tốt - vẽ hai bước" cho hình chóp S.GBC với G là "điểm tốt" ta có:
\(\dfrac{1}{x^2}=\dfrac{1}{SG^2}+\dfrac{1}{GM^2}=\dfrac{1}{a^2}+\dfrac{1}{\left(a\dfrac{\sqrt{3}}{6}\right)^2}\)
\(\Rightarrow x=\dfrac{a}{\sqrt{13}}\)
Mô hình "điểm tốt - vẽ hai bước": Cho hình chóp S.ABC với \(SA\perp\left(ABC\right)\). Kẻ \(AH\perp BC,AK\perp SH\) thì d(A,(SBC))=AK.
CM: Ta có: \(SA\perp\left(ABC\right)\Rightarrow SA\perp AH\)
Mà \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)
\(\Rightarrow\left(SBC\right)\perp\left(SAH\right)\) theo giao tuyến SH
Mà \(AK\perp SH,AK\subset\left(SAH\right)\) \(\Rightarrow AK\perp\left(SBC\right)\), dễ dàng suy ra đpcm

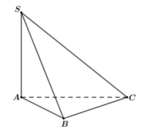
Đáp án A
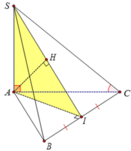
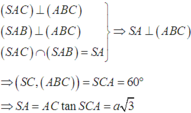
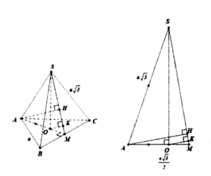
Gọi I,H lần lượt là hình chiếu vuông góc của A trên BC, SI, khi đó: d(A, (SBC)) =AH
Tam giác ABC đều cạnh a nên AI = a 3 2
Khi đó xét tam giác SAI :
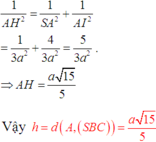

Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)

Chọn C
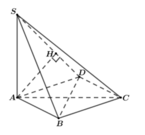
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
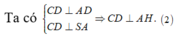
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có