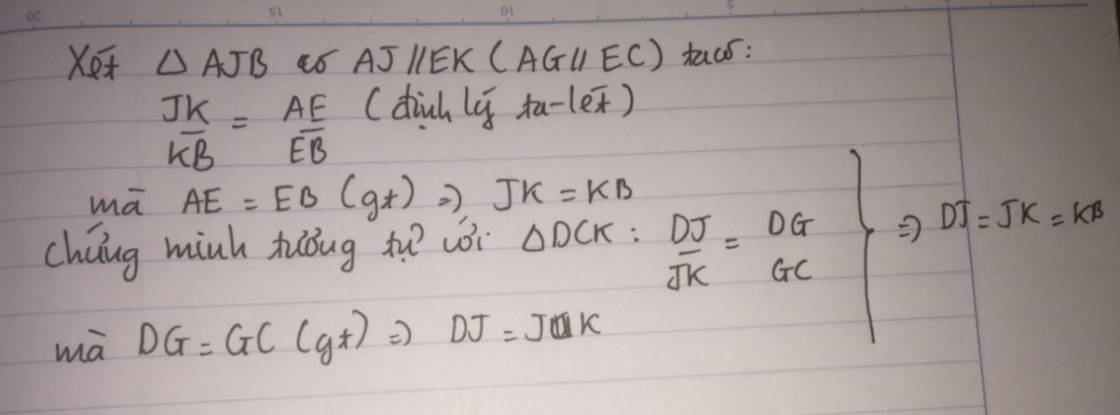Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F T G
íu biết thì cut hộ
Gọi T,G là giao điểm DE,BF với AC
Ta có:AB=CD nên \(\frac{1}{2}AB=\frac{1}{2}CD\Rightarrow EB=DF\) mà \(EB//DF\) nên tứ giác EBFD là hình bình hành => ED//BF
Xét \(\Delta\)ABG có EA=EB;ET//BG nên T là trung điểm AG hay TA=TG ( 1 )
Xét \(\Delta\)CDT có FD=FC;FG//DT nên G là trung điểm CT hay TG=GC ( 2 )
Từ ( 1 ) và ( 2 ) suy ra đpcm

dễ dàng chứng minh được EBFD là hình bình hành => FB // DE
gọi I là giao điểm của DE và AC ; K là giao điểm của FB và AC
ta có: FB là đường trung bình của tam giác DIC => FB chia IC thành hai đoạn bằng nhau (1)
tương tự chứng minh được DE là đường trung bình của tam giác AKB => DE chia AK thành hai đoạn bằng nhau (2)
Từ 1 và 2 => đpcm
*Bên trên là gợi ý thôi bạn tự trình bày nhé =))))

b) Gọi giao điểm của BD với AG ; AF là J;H
DG//AB ; AG ∩ DB = J
Áp dụng định lí Talet ta có :
\(\frac{DG}{AB}=\frac{DJ}{JB}=\frac{1}{2}\Rightarrow DJ=\frac{1}{2}.JB\)
=> DJ = \(\frac{1}{3}.DB\)
amtt HB = \(\frac{1}{3}.DB\)
Mà DJ + JH + HB = DB
=> JH = 1/3 . BD
=> DJ = JH= HB
=> AG; AF chia BD thành 2 đoạn bằng nhau => đpcm

Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF
Xét ΔABN có
E là trung điểm của AB
EM//NB
Do đó: M là trung điểm của AN
hay AM=MN(1)
Xét ΔDCD có
F là trung điểm của CD
FN//MD
DO đó: N là trung điểm của MC
Suy ra: MN=NC(2)
Từ (1) và (2) suy ra AM=MN=NC

DEBF có EB // DF ; EB = \(\frac{1}{2}\).AB = \(\frac{1}{2}\).DC = FC
=> DEBF là hình bình hành
A B C D E F M N 1 2 1 2
Vì AB = CD (định lý)
mà EA = EB = FD = FC
Ta có :
AB // CD (gt) => EB // DF
=> EBFD là hình bình hành