Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
\(CF=FD=\dfrac{CD}{2}\)(F là trung điểm của CD)
mà AB=CD(Hai cạnh đối của hình bình hành ABCD)
nên AE=CF=FD=EB
Xét tứ giác AECF có
AE//CF(AB//CD, E∈AB, F∈CD)
AE=CF(cmt)
Do đó: AECF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác AEFD có
AE//FD(AB//CD, E∈AB, F∈CD)
AE=FD(cmt)
Do đó: AEFD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
c) Ta có: AF//CE(Hai cạnh đối trong hình bình hành AECF)
mà H∈AF(gt)
và K∈CE(gt)
nên HF//KC và EK//AH
Xét ΔDKC có
F là trung điểm của CD(gt)
FH//DK(cmt)
Do đó: H là trung điểm của DK(Định lí 1 về đường trung bình của tam giác)
⇒DH=KH(1)
Xét ΔABH có
E là trung điểm của AB(gt)
EK//BH(cmt)
Do đó: K là trung điểm của BH(Định lí 1 về đường trung bình của tam giác)
⇒BK=KH(2)
Từ (1) và (2) suy ra DH=HK=KB(đpcm)

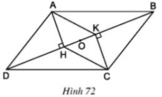
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.

a, ABCD là hình bình hành (gt) \(\Rightarrow\hept{\begin{cases}AD//BC\\AD=BC\end{cases}}\Rightarrow\hept{\begin{cases}\widehat{ADH}=\widehat{CBK}\\AD=BC\end{cases}}\)
\(\Delta ADH=\Delta CBK\left(ch-gn\right)\Rightarrow AH=CK\left(1\right)\) ( 2 cạnh tương ứng )
b, \(AH\perp BD,CK\perp BD\left(gt\right)\Rightarrow AH//CK\left(2\right)\)
ABCD là hình bình hành có O là trung điểm của đường chéo BD (gt) nên O là trung điểm của AC.
Từ (1) và (2) \(\Rightarrow AHCK\) là hình bình hành.
Mà O là trung điểm của đường chéo AC nên O là trung điểm của HK (t/c hình bình hành)
Chúc bạn học tốt.
nhanh 3 k miễn phí mai nhớ cổ vũ đội bóng việt nam nha
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.